FIND THE EQUATION OF PERPENDICULAR BISECTOR

Question 1 :

Find the equation of the perpendicular bisector of the straight line segment joining the points (3,4) and (-1,2)

Solution :

midpoint of the line segment joining the points (3,4) and (-1,2)

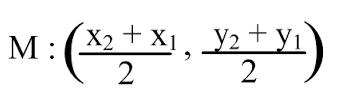
x₁ = 3, y₁ = 4, x₂ = -1 , y₂ = 2

  =  [(x₁ + x₂)/2 , (y₁ + y₂)/2]

  =  (3 + (-1))/2 , (4 + 2)/2

  =  (2/2, 6/2)

  =  (1 , 3)

slope of the line joining the points (3,4) and (-1,2)

m  =  (y₂ - y₁)/(x₂ - x₁)

  =  (2 - 4)/(-1-3)

  =  -2/(-4)

  =  1/2

Slope of the required line  =  -1/(1/2)

  =  -2

Equation of the required line :

(y - y₁)/(y₂ - y₁) =   (x - x₁)/(x₂ - x₁)

(y - 4)/(2 - 4) = (x - 3)/(-1 - 3)

(y - 4)/(-2) = (x - 3)/(-4)

-4(y - 4) = -2(x - 3)

- 4 y + 16 = - 2 x + 6

2 x -4 y + 16 - 6 = 0

2 x - 4 y + 10 = 0

dividing the whole equation by 2, we get

x - 2 y - 5 =0

Finding the Intersection of Two Lines and Parallel to the Line Passing Through the Points

Question 2 :

Find the equation of the straight line passing through the point of intersection of the lines 2x+y-3=0 and 5x  + y - 6 = 0 and parallel to the line joining the points (1,2) and (2,1)

Solution :

To find the point of intersection of any two lines we need to solve them

2x + y - 3 = 0 ---- (1)

5x  + y - 6 = 0 ---- (2)

(1) - (2)

          2x + y - 3 = 0

          5x  + y - 6 = 0

           (-)  (-)  (+)

        ----------------- 

          - 3x + 3 = 0

            - 3 x = -3

                x = 1

Substitute x = 1 in the first equation

2(1) + y - 3 = 0

-1 + y = 0

y = 1

the point of intersection is (1,1)

The required line is parallel to the line joining the points (1, 2) and (2, 1). So their slopes will be equal.

m  =  (y₂ - y₁)/(x₂ - x₁)

  =  (1-2)/(2-1)

  =  -1/1  = -1

Slope of the required line is -1 and a point on the line is (1, 1)

Equation of the Line :

(y - y₁) = m (x - x₁)

(y - 1) = -1 (x - 1)

y - 1 = - x + 1

x + y - 1 - 1 = 0

x + y - 2 = 0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.