FIND THE EQUATION OF THE LINE EXAMPLES

Example 1 :

A cat is located at the point(-6, -4) in xy plane. A bottle of milk is kept at (5, 11). The cat wishes to consume the milk travelling through shortest possible distance. Find the equation of the path it needs to take its milk.

Solution :

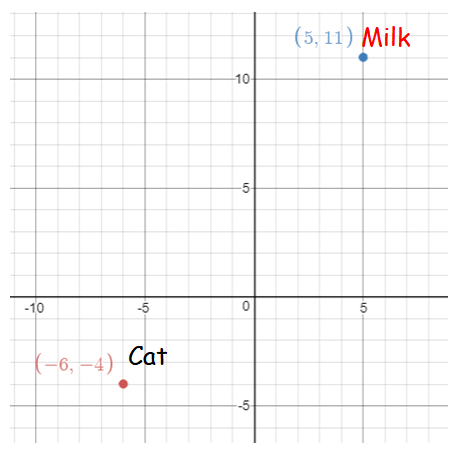
Equation of the path :

(y - y₁)/(y₂ - y₁)  =  (x - x₁)/(x₂ - x₁)

Substitute (x₁, y₁) = (-6, -4) and (x₂, y₂) = (5, 11).

(y + 4)/(11 + 4)  =  (x + 6)/(5 + 6)

(y + 4)/15  =  (x + 6)/11

11(y + 4)  =  15(x + 6)

11y + 44  =  15x + 90

15x - 11y + 90 - 44  =  0

15x - 11y + 46  =  0

Example 2 :

Find the equation of the median and altitude of triangle ABC through A where the vertices are A(6, 2), B(-5, -1) and C(1, 9).

Solution :

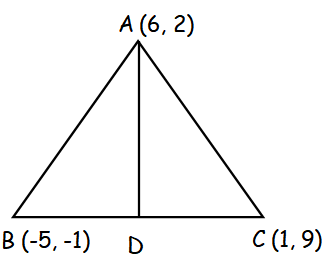
The median drawn passing through the vertex A intersect the side BC at the midpoint. 

D  =  (x₁ + x₂)/2, (y₁ + y₂)/2

Substitute (x₁, y₁) = (-5, -1) and (x₂, y₂) = (1, 9).

D  =  (-5 + 1)/2, (-1 + 9)/2

  =  -4/2, 8/2

  =  D (-2, 4)

Equation of the median AD :

(y - y₁)/(y₂ - y₁)  =  (x - x₁)/(x₂ - x₁)

Substitute (x₁, y₁) = A(6, 2) and (x₂, y₂) = D(-2, 4).

(y - 2)/(4 - 2)  =  (x - 6)/(-2 - 6)

(y - 2)/2  =  (x - 6)/(-8)

-8(y - 2)  =  2(x - 6)

-8y + 16  =  2x - 12

2x + 8y - 12 - 16  =  0

2x + 8y - 28  =  0

Dividing the entire equation by 2, we get

x + 4y - 14  =  0

If a line passing through the vertex A is altitude, then it will be perpendicular to BC.

Slope of BC :

m = (y₂ - y₁)/(x₂ - x₁)

Substitute (x₁, y₁) = B(-5, -1) and (x₂, y₂) = C(1, 9).

m = (9 + 1)/(1 + 5)

m = 10/6  =  5/3

Equation of altitude passing through A.

(y - y₁)  =  m(x - x₁)

(x₁, y₁) = A(6, 2)  m = 5/3

(y - 2) =  (5/3)(x - 6)

3(y - 2)  =  5(x - 6)

3y  - 6  =  5x - 30

5x - 3y - 30 + 6  =  0

5x - 3y - 24  =  0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.