FIND THE EQUATION OF THE TANGENT AND NORMAL TO THE GIVEN CURVE
Tangent :
The tangent line (or simply tangent) to a plane curve at a given point is the straight line that just touches the curve at that point.
Equation of tangent :
(y-y1) = m(x-x1)
Normal :
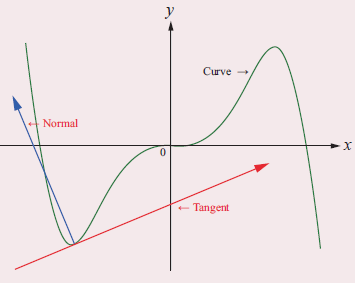
The normal at a point on the curve is the straight line which is perpendicular to the tangent at that point. The tangent and the normal of a curve at a point are illustrated in the adjoining figure.
Equation of normal :
(y-y1) = (-1/m)(x-x1)
Find the tangent and normal to the following curves at the given points on the curve.
(i) y = x2 - x4 at (1, 0)
Solution :
y = x2 - x4
Differentiating with respect to x, we get
dy/dx = 2x-4x3
Slope at (1, 0)
dy/dx = 2(1)-4(1)3
dy/dx = -2
Slope of tangent = -2
Slope of normal = 1/2
Equation of tangent :
(y-y1) = m(x-x1)
(y-0) = -2(x-1)
y = -2x+2
2x+y-2 = 0
So, the equation of tangent is 2x+y-2 = 0.
Equation of normal :
(y-y1) = (-1/m)(x-x1)
(y-0) = (1/2)(x-1)
2y = x-1
x-2y-1 = 0
So, equation of normal is x-2y-1 = 0.
(ii) y = x4+2ex at (0, 2)
Solution :
dy/dx = 4x3 + 2ex
Slope at (0, 2)
dy/dx = 4(0)3 + 2e0
dy/dx = 2
Slope of the tangent = 2
Slope of the normal = -1/2
Equation of tangent :
(y-2) = 2(x-0)
y-2 = 2x
2x-y+2 = 0
Equation of normal :
(y-2) = (-1/2)(x-0)
2(y-2) = -x
2y-4 = -x
x+2y-4 = 0
So, equation of tangent is 2x-y+2 = 0 and equation of normal is x+2y-4 = 0.
(iii) y = x sin x at (π/2, π/2)
Solution :
y = x sin x
dy/dx = x cos x + sin x (1)
dy/dx = x cos x + sin x
dy/dx at (π/2, π/2)
dy/dx = π/2 cos π/2 + sin π/2
dy/dx = π/2 (0) + 1
dy/dx = 1
Slope of tangent = 1
Slope of normal = -1
Equation of tangent :
(y - π/2) = 1(x - π/2)
y - π/2 = x - π/2
x-y = 0
Equation of normal :
(y - π/2) = -1(x - π/2)
y - π/2 = -x + π/2
x+y-π = 0
(iv) x = cost, y = 2 sin2t at t = π/3
Solution :
|
x = cost dx/dt = -sin t |
y = 2 sin2t dy/dt = 4 sin t cost |
dy/dx = (dy/dt) / (dx/dt)
dy/dx = 4 sin t cost / (-sin t)
dy/dx = -4 cost
dy/dx at t = π/3 = -4cos (π/3)
= -4(1/2)
= -2
Slope of tangent = -2
Slope of normal = -1/(-2) ==> 1/2
|
x = cost x = cos ( π/3) x = 1/2 |
y = 2 sin2t y = 2 sin2(π/3) y = 2 (3/4) y = 3/2 |
Equation of tangent :
(y-(3/2)) = -2(x-(1/2))
(2y-3) = -2(2x-1)
2y-3 = -4x+2
4x+2y-5 = 0
Equation of normal :
(y-(3/2)) = (1/2)(x-(1/2))
2(2y-3) = (2x-1)
4y-6 = 2x-1
2x-4y-1+6 = 0
2x-4y+5 = 0

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions (Part - 8)
Jan 30, 25 09:48 AM
AP Calculus AB Problems with Solutions (Part - 8) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Jan 29, 25 06:00 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 105)
Jan 29, 25 05:52 AM
Digital SAT Math Problems and Solutions (Part - 105)