FIND THE EQUILIBRIUM POINT OF THE DEMAND AND SUPPLY EQUATIONS

Definition for equilibrium, equilibrium price, and equilibrium point :

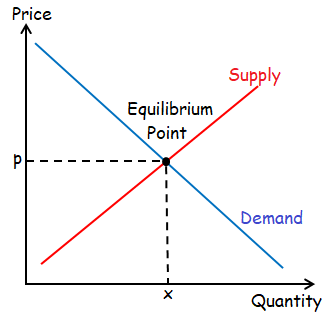
Equilibrium :

Equilibrium is the state in which market supply and demand each other, and as a result prices become a stable. The balancing effect of supply and demand results in a state of equilibrium.

Equilibrium price :

The equilibrium price is the market price where the quantity of goods supplied is equal to the quantity of goods demanded.

Equilibrium point :

The equilibrium point, (x_E, p_E), is the point at which the supply and demand curves intersect.

where,

x  =  number of units

p  =  price in dollars

Example 1  :

Nibok manufacturing has determined that production and price of a new tennis should be geared to the equilibrium point for this system of equations.

p  =  160 - 5x (Demand curve)

p  =  35 + 20x (Supply curve)

Solution  :

Given two equations,

Demand curve =====> p  =  160 - 5x -----(1)

Supply curve =====> p  =  35 + 20x -----(2)

We find the equilibrium point for this system of equations.

The equilibrium point is the ordered pair (x, p) that is obtained by solving the system of demand and supply equations.

Then,

By equating the two equations (1) and (2), we get

160 - 5x  =  35 + 20x

160 - 35  =  20x + 5x

125  =  25x

x  =  5

By applying x  =  5 in equation (1), we get

p  =  160 - 5x

p  =  160 - 5(5)

p  =  160 - 25

p  =  135

So, the equilibrium point is (5, 135)

Example 2  :

Find the equilibrium point for the given demand and supply curve.

p  =  200 - 15x (Demand curve)

p  =  50 + 25x (Supply curve)

Solution  :

Given two equations,

Demand curve =====> p  =  200 - 15x -----(1)

Supply curve =====> p  =  50 + 25x -----(2)

We find the equilibrium point for this system of equations.

Then,

By equating the two equations (1) and (2), we get

200 - 15x  =  50 + 25x

200 - 50  =  25x + 15x

150  =  40x

x  =  3.75

By applying x  =  3.75 in equation (1), we get

p  =  200 - 15x

p  =  200 - 15(3.75)

p  =  200 - 56.25

p  =  143.75

So, the equilibrium point is (3.75, 143.75)

Example 3  :

Find the equilibrium point for the given demand and supply curve.

p  =  15 - (7/100)x (Demand curve)

p  =  2 + (3/100)x (Supply curve)

Solution  :

Given two equations,

Demand curve =====> p  =  15 - (7/100)x -----(1)

Supply curve =====> p  =  2 + (3/100)x -----(2)

Then,

By equating the two equations (1) and (2), we get

15 - (7/100)x  =  2 + (3/100)x

15 - 2  =  [3/100 + 7/100]x

13  =  (1/10)x

x  =  130

By applying x  =  130 in equation (1), we get

p  =  15 - (7/100)x

p  =  15 - (7/100)(130)

p  =  15 - (91/10)

p  =  (150 - 91)/10

p  =  5.9

So, the equilibrium point is (130, 5.9)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.