FIND THE GRADIENT OF A LINE FROM THE TWO POINTS

Gradient between two points :

The gradient of a line is the slope of the line.

If given two points  (x₁, y₁) and (x₂, y₂), then

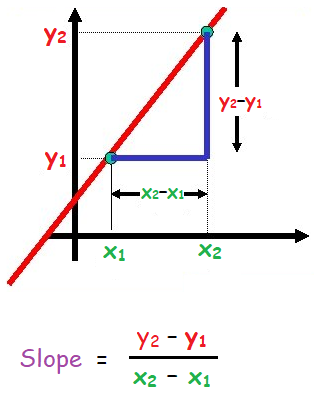
Find the gradient of the line segment joining the following pairs of points:

Problem 1 :

(2, 1) and (5, 2)

Solution :

Let A(2, 1) and B(5, 2) be the two points.

If A is (x₁, y₁) and B is (x₂, y₂), then

Slope of AB  =  (y₂ – y₁)/(x₂ – x₁)

Here  x₁  =  2,  x₂  =  5, y₁  =  1,  y₂  =  2

=  (2 – 1)/(5 – 2)

=  1/3

Problem 2 :

(5, 3) and (2, 2)

Solution :

Let A(5, 3) and B(2, 2) be the two points.

If A is (x₁, y₁) and B is (x₂, y₂), then

Slope of AB  =  (y₂ – y₁)/(x₂ – x₁)

Here x₁  =  5,  x₂  =  2,  y₁  =  3,  y₂  =  2

=  (2 – 3)/(2 – 5)

=  -1/-3

=  1/3

Problem 3 :

(2, -2) and (4, 1)

Solution :

Let A(2, -2) and B(4, 1) be the two points.

If A is (x₁, y₁) and B is (x₂, y₂), then

Slope of AB  =  (y₂ – y₁)/(x₂ – x₁)

let  x₁  =  2,  x₂  =  4,  y₁  =  -2,  y₂  =  1

=  (1 + 2)/(4 – 2)

=  3/2

Problem 4 :

(7, 2) and (-3, 2)

Solution :

Let A(7, 2) and B(-3, 2) be the two points.

Slope of AB  =  (y₂ – y₁)/(x₂ – x₁)

Here x₁  =  7, x₂  =  -3,  y₁  =  2,  y₂  =  2

=  (2 – 2)/(-3 – 7)

=  0/-10

=  0

Problem 5 :

(-6, -2) and (-6, -4)

Solution :

Let A(-6, -2) and B(-6, -4) be the two points.

Slope of AB  =  (y₂ – y₁)/(x₂ – x₁)

Here x₁  =  -6, x₂  =  -6,  y₁  =  -2,  y₂  =  -4

=  (-4 + 2)/(-6 + 6)

=  -2/0

=  undefined

Problem 6 :

(5, -1) and (-3, -3)

Solution :

Let A(5, -1) and B(-3, -3) be the two points.

Slope of AB  =  (y₂ – y₁)/(x₂ – x₁)

Here x₁  =  5, x₂  =  -3,  y₁  =  -1,  y₂  =  -3

=  (-3 + 1)/(-3 - 5)

=  -2/-8

=  1/4

Problem 7 :

(-5, 4) and (4, 0)

Solution :

Let A(-5, 4) and B(4, 0) be the two points.

Slope of AB  =  (y₂ – y₁)/(x₂ – x₁)

Here x₁  =  -5, x₂  =  4,  y₁  =  4,  y₂  =  0

=  (0 – 4)/(4 + 5)

=  -4/9

Problem 8 :

(0, -5) and (-2, -3)

Solution :

Let A(0, -5) and B(-2, -3) be the two points.

Slope of AB  =  (y₂ – y₁)/(x₂ – x₁)

Here x₁  =  0, x₂  =  -2,  y₁  =  -5,  y₂  =  -3

=  (-3 + 5)/(-2 – 0)

=  2/-2

=  -1

Problem 9 :

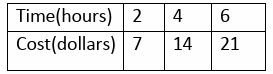
The table shows the cost of using a computer at an Internet café for a given amount of time. Find the rate of change in cost with respects to time

Solution :

To find the rate of change, we use the formula 

change in y / change in x

Selecting two points from the table, (2, 7) and (4, 14)

Change in y = 14 - 7 ==> 7

Change in x = 4 - 2 ==> 2

Rate of change = 7/2

= 3.5

So, the required rate of change is $3.5 per hour.

Problem 10 :

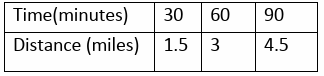
The table shows the distance a person walks for exercise. Find the rate of change in distance with respect to time

Solution :

Selecting two points from the table, (30, 1.5) and (60, 3)

Change in y = 3 - 1.5 ==> 1.5

Change in x = 60 - 30 ==> 30

Rate of change = 1.5/30

= 0.05

So, the rate of change is 0.05 miles per minute.

Problem 11 :

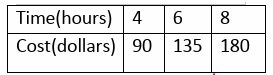
The table shows the cost to paint a house for a given number of hours. Find the rate of change in cost with respect to time .

Solution :

Selecting two points from the table, (4, 90) and (6, 135)

Change in y = 135 - 90 ==> 45

Change in x = 6 - 4 ==> 2

Rate of change = 45/2

= 22.5

So, the rate of change is 0.05 miles per minute.

Problem 12 :

The value of a car decreases at a constant rate. After 3 years, the value of the car is $15,000. After 2 more years the value of the car is $11,000.

a. Write an equation that represents the value y (in dollars) of the car after x years.

b. What is the y-intercept of the line? Interpret the y-intercept.

Solution :

a)  (3, 15000) and (5, 11000)

Slope = (11000 - 15000)/(5 - 3)

= -4000/2

= -2000

Equation will be in the form of y = mx + b

Here m = -2000 and one of the points on the line is (3, 15000)

y = -2000x + b

15000 = -2000(3) + b

15000 + 6000 = b

b = 21000

Applying the y-intercept, we get

y = -2000x + 21000

b)

y -intercept :

Put x = 0

y = -2000(0) + 21000

y = 21000

x-intercept :

Put y = 0

0 = -2000x + 21000

-21000 = -2000x

x = 21000/2000

x = 10.5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.