FIND THE INTERVALS ON WHICH EACH FUNCTION IS CONTINUOUS

Three requirements have to be satisfied for the continuity of a function y = f(x) at x = x₀ :

(i) f(x) must be defined in a neighbourhood of x₀ (i.e., f(x₀) exists);

(ii) lim _x->x₀  f(x) exists.

(iii) f(x₀)  =  lim _{x ->} x₀ f(x)

To know the points to be remembered in order to decide whether the function is continuous at particular point or not, you may look into the page " How to Check Continuity of a Function If Interval is not Given "

Question 1 :

Examine the continuity of the following 

sin x / x²

Solution :

Let f(x)  =  sin x / x²

(i)  From the given function, we know that both "x" and "sin x " are defined for all real numbers. Here "x" is in the denominator, so it should not be 0.

(ii)  lim _{x-> x0} f(x)  =  lim _{x-> x0} sin x / x²

By applying the limit, we get

 =  sin x₀ / (x₀)² -------(1)

(iii) f(x₀)  =   sin x₀ / (x₀)² -------(2)

From (1) and (2)

lim _{x-> x0} f(x)  =  f(x₀)

Hence the given function is continuous for all x ∈ R - {0}.

Question 2 :

Examine the continuity of the following 

(x² - 16) / (x + 4)

Solution :

Let f(x)  =  (x² - 16) / (x + 4)

If we apply x = -4, then the denominator will become zero. So the entire value will become infinity.

Hence it is continuous for all x ∈ R - {-4}.

Question 3 :

Examine the continuity of the following 

|x + 2| + |x - 1|

Solution :

Since we have a absolute value function, we have to split into piece wise function and check its continuity.

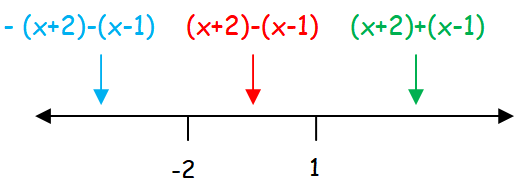
f(x)  =  -x - 2 - x + 1  =  -2x - 1     If x < -2

f(x)  =  x + 2 - x + 1  =  3      If -2 ≤ x < 1

f(x)  =  x + 2 + x - 1  =  2x + 1   If x ≥ 1

From the above piece wise unction, we have to check if it is continuous at x = -2 and x = 1

Since left hand limit and right hand limit are equal for -2, it is continuous at x = -2.

Since left hand limit and right hand limit are equal for 1, it is continuous at x = 1.

Hence the function is continuous for x ∈ R

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.