FIND THE INVERSE OF A SQUARE MATRIX
Example 1 :
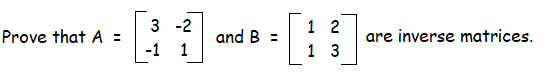
Solution :
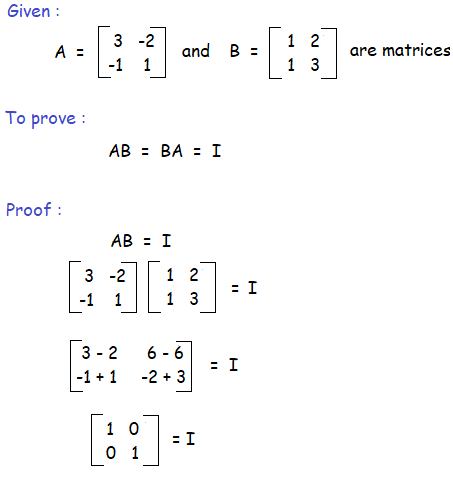
So, AB = BA = I (Identity matrix)
Hence proved.
Example 2 :
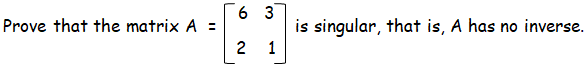
Solution :
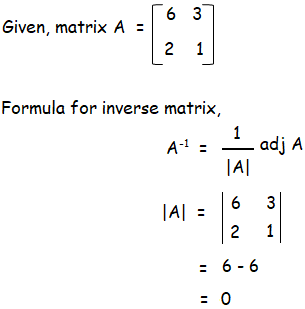
Since |A| = 0, it is singular matrix, A-1 does not exists.
So, there is no inverse matrix of A.
Hence proved.
Example 3 :

Solution :

Example 4 :

Solution :

Example 5 :

Solution :

Example 6 :

Solution :

|A| = +2(0 - 4) - 3(-1 + 0) - 1(-1 + 0)
= -8 + 3 + 1
= -8 + 4
|A| = -4
-4 ≠ 0
Since |A| = -4 ≠ 0, it is non singular matrix. A-1 exists.

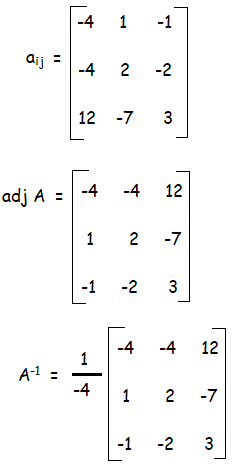
Example 7 :
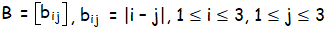
Solution :
General term :
bij = = |i – j|
(where 1 ≤ i ≤ 3, 1 ≤ j ≤ 3)
Number of rows of the required matrix is 3.
Number of columns of the required matrix is 3.
Finding the elements :
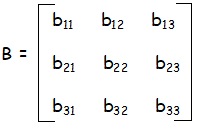
|
bij = |i – j| b11 = |1 – 1| b11 = 0 |
bij = |i – j| b12 = |1 – 2| b12 = 1 |
bij = |i – j| b13 = |1 – 3| b12 = 2 |
|
bij = |i – j| b21 = |2 – 1| b21 = 1 |
bij = |i – j| b22 = |2 – 2| b22 = 0 |
bij = |i – j| b23 = |2 – 3| b23 = 1 |
|
bij = |i – j| b31 = |3 – 1| b31 = 2 |
bij = |i – j| b32 = |3 – 2| b32 = 1 |
bij = |i – j| b33 = |3 – 3| b33 = 0 |
Hence the required matrix is
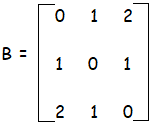
Finding the inverse matrix of B :
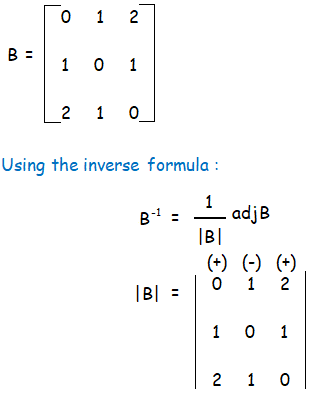
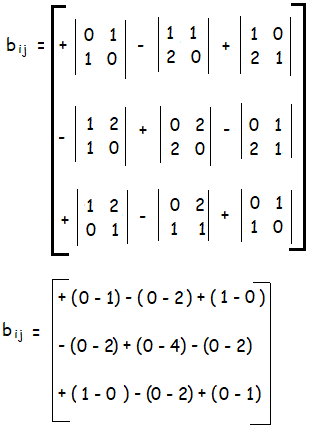
|B| = + 0(0 - 1) - 1(0 - 2) + 2(1 - 0)
= 2 + 2
= 4
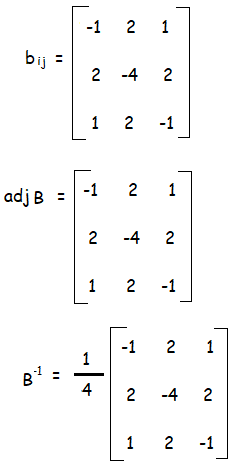
Since |B| = 4 ≠ 0, it is non singular matrix. B-1 exists.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 146)
Apr 18, 25 06:52 AM
Digital SAT Math Problems and Solutions (Part - 146) -
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145)

