FIND THE LEAST NUMBER SHOULD BE DIVIDED TO GET A PERFECT SQUARE

Example 1 :

Find the least number multiplied by 200 to get a perfect square.

Solution :

Decompose 200 into its prime factors.

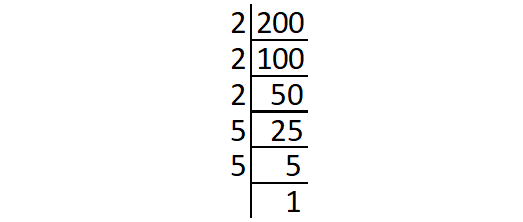
Prime factors of 200 :

200 = 2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5

= (2 ⋅ 2) ⋅ 2 ⋅ (5 ⋅ 5)

The prime factor 2 does not occur in pair.

So, '2' is the least number by which 200  has to be divided to get a perfect square.

Justification :

√(200/2) = √[(2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5)/2]

√100 = √(2 ⋅ 2 ⋅ 5 ⋅ 5)

= 2 ⋅ 5

= 10

Further,

200/2 = 100 = 10²

Example 2 :

Find the least number by which 252 has to be divided to get a perfect square.

Solution :

Decompose 252 into its prime factors.

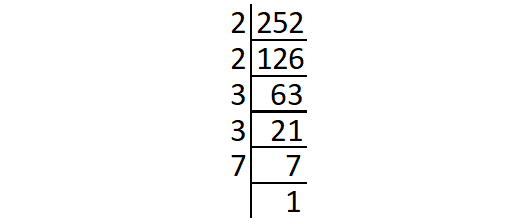
Prime factors of 252 :

252 = 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 7

= (2 ⋅ 2) ⋅ (3 ⋅ 3) ⋅ 7

The prime factor 7 does not occur in pair.

So, '7' is the least number by which 252 has to divided to get a perfect square.

Justification :

√(252/7) = √[(2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 7)/7]

√36 = √(2 ⋅ 2 ⋅ 3 ⋅ 3)

= 2 ⋅ 3

= 6

Further,

252/7 = 36 = 6²

Example 3 :

Find the least number multiplied by 1620 to get a perfect square.

Solution :

Decompose 1620 into its prime factors.

Prime factors of 1620 :

1620 = 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 5

= (2 ⋅ 2) ⋅ (3 ⋅ 3) ⋅ (3 ⋅ 3) ⋅ 5

The prime factor 5 does not occur in pair.

So, '5' is the least number to be multiplied by 180 to get a perfect square.

Justification :

√(1620/5) = √[(2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 5)/5]

√324 = √(2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3)

= 2 ⋅ 3 ⋅ 3

= 18

Further,

1620/5 = 324 = 18²

Example 4 :

Find the least number multiplied by 2925 to get a perfect square.

Solution :

Decompose 2925 into its prime factors.

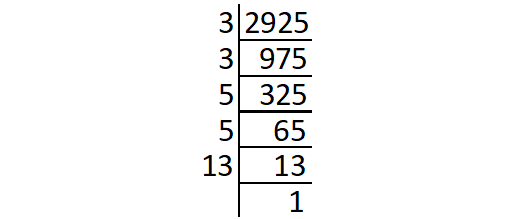
Prime factors of 2925 :

2925 = 3 ⋅ 3 ⋅ 5 ⋅ 5 ⋅ 13

= (3 ⋅ 3) ⋅ (3 ⋅ 3) ⋅ 13

The prime factor 13 does not occur in pair.

So, '13' is the least number by which 2925 has to be divided to get a perfect square.

Justification :

√(2925/13) = √[(3 ⋅ 3 ⋅ 5 ⋅ 5 ⋅ 13)/13]

√225 = √(3 ⋅ 3 ⋅ 5 ⋅ 5)

= 3 ⋅ 5

= 15

Further,

2925/5 = 225 = 15²

Example 5 :

Find the least number multiplied by 384 to get a perfect square.

Solution :

Decompose 384 into its prime factors.

Prime factors of 384 :

384 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3

= (2 ⋅ 2) ⋅ (2 ⋅ 2) ⋅ (2 ⋅ 2) ⋅ 2 ⋅ 3

The prime factors 2 and 3 do not occur in pair.

Product of 2 and 3 :

2 ⋅ 3 = 6

So, '6' is the least number by which 384 has to be divided to get a perfect square.

Justification :

√(384/6) = √[2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3)/6]

√64 = √[2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3)/(2 ⋅ 3)]

= √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2)

= 2 ⋅ 2 ⋅ 2

= 8

Further,

384/6 = 64 = 8²

Example 6 :

Find the least number by which 120 has to be divided to get a perfect square.

Solution :

Decompose 120 into its prime factors.

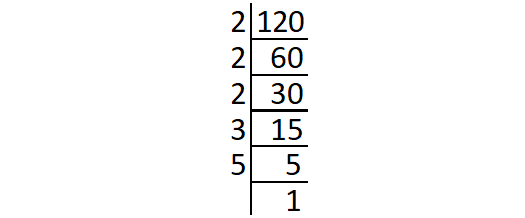
Prime factors of 120 :

120 = 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 5

= (2 ⋅ 2) ⋅ 2 ⋅ 3 ⋅ 5

The prime factors 2, 3 and 5 do not occur in pair.

Product of 2, 3 and 5 :

2 ⋅ 3 ⋅ 5 = 30

So, '30' is the least number by which 120 has to be divided to get a perfect square.

Justification :

√(120/30) = √[(2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 5)/30]

√4 = √[(2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 5)/(2 ⋅ 3 ⋅ 5)]

= √(2 ⋅ 2)

= 4

Further,

120/30 = 4 = 2²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.