FIND THE LEAST NUMBER SHOULD BE MULTIPLIED TO GET A PERFECT SQUARE

Example 1 :

Find the least number multiplied by 200 to get a perfect square.

Solution :

Decompose 200 into its prime factors.

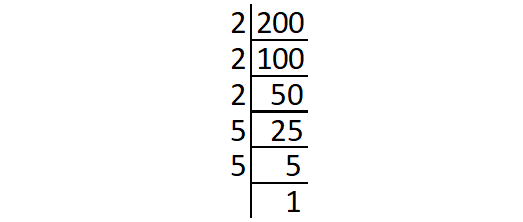
Prime factors of 200 :

200 = 2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5

= (2 ⋅ 2) ⋅ 2 ⋅ (5 ⋅ 5)

The prime factor 2 does not occur in pair.

So, '2' is the least number to be multiplied by 200 to get a perfect square.

Justification :

√[2(200)] = √[2(2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5)]

√400 = √[(2 ⋅ 2)(2 ⋅ 2)(5 ⋅ 5)]

= 2 ⋅ 2 ⋅ 5

= 20

Further,

2(200) = 400 = 20²

Example 2 :

Find the least number multiplied by 252 to get a perfect square.

Solution :

Decompose 252 into its prime factors.

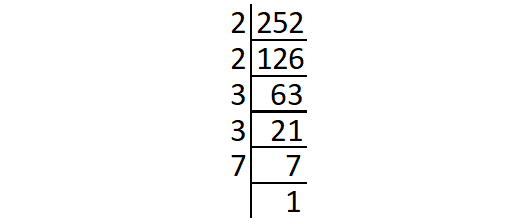
Prime factors of 252 :

252 = 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 7

= (2 ⋅ 2) ⋅ (3 ⋅ 3) ⋅ 7

The prime factor 7 does not occur in pair.

So, '7' is the least number to be multiplied by 252 to get a perfect square.

Justification :

√[7(252)] = √[7(2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 7)]

√1764 = √[(2 ⋅ 2)(3 ⋅ 3)(7 ⋅ 7)]

= 2 ⋅ 3 ⋅ 7

= 42

Further,

7(252) = 1764 = 42²

Example 3 :

Find the least number multiplied by 180 to get a perfect square.

Solution :

Decompose 180 into its prime factors.

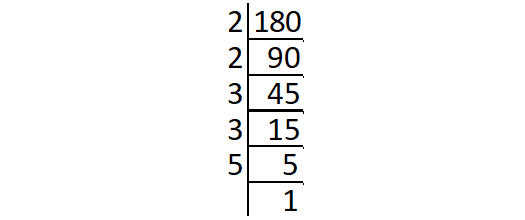
Prime factors of 180 :

180 = 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 5

= (2 ⋅ 2) ⋅ (3 ⋅ 3) ⋅ 5

The prime factor 5 does not occur in pair.

So, '5' is the least number to be multiplied by 180 to get a perfect square.

Justification :

√[5(180)] = √[5(2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 5)]

√900 = √[(2 ⋅ 2)(3 ⋅ 3)(5 ⋅ 5)]

= 2 ⋅ 3 ⋅ 5

= 30

Further,

5(180) = 900 = 30²

Example 4 :

Find the least number multiplied by 90 to get a perfect square.

Solution :

Decompose 90 into its prime factors.

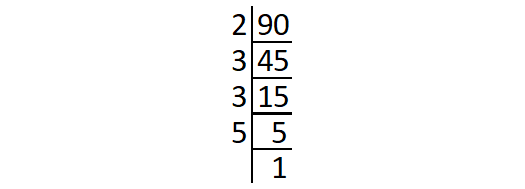
Prime factors of 90 :

90 = 2 ⋅ 3 ⋅ 3 ⋅ 5

= 2 ⋅ (3 ⋅ 3) ⋅ 5

The prime factors 2 and 5 do not occur in pair.

Product of 2 and 5 :

2 ⋅ 5 = 10

So, '10' is the least number to be multiplied by 90 to get a perfect square.

Justification :

√[10(90)] = √[10(2 ⋅ 3 ⋅ 3 ⋅ 5)]

√900 = √[(2 ⋅ 5)(2 ⋅ 3 ⋅ 3 ⋅ 5)]

= √[(2 ⋅ 2)(3 ⋅ 3)(5 ⋅ 5)]

= 2 ⋅ 3 ⋅ 5

= 30

Further,

10(90) = 900 = 30²

Example 5 :

Find the least number multiplied by 120 to get a perfect square.

Solution :

Decompose 120 into its prime factors.

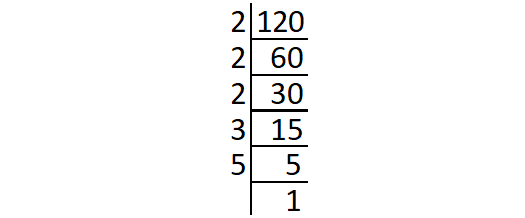
Prime factors of 120 :

120 = 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 5

= (2 ⋅ 2) ⋅ 2 ⋅ 3 ⋅ 5

The prime factors 2, 3 and 5 do not occur in pair.

Product of 2, 3 and 5 :

2 ⋅ 3 ⋅ 5 = 30

So, '30' is the least number to be multiplied by 120 to get a perfect square.

Justification :

√[30(120)] = √[30(2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 5)]

√3600 = √[(2 ⋅ 3 ⋅ 5)(2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 5)]

= √[(2 ⋅ 2)(2 ⋅ 2)(3 ⋅ 3)(5 ⋅ 5)]

= 2 ⋅ 2 ⋅ 3 ⋅ 5

= 60

Further,

30(120) = 3600 = 60²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.