FIND THE LEAST NUMBER TO BE ADDED TO GET A PERFECT SQUARE

Example 1 :

Find the least number which must be added to 104979 so as to get a perfect square.

Solution :

Find the square root of 104979 using long division method.

Step 1 :

Separate the digits by taking commas from right to left once in two digits.

10,49,79

When we do so, we get 10 before the first comma.

Step 2 :

Now we have to multiply a number by itself such that

the product ≤ 10

(The product must be greatest and also less than 10)

The above condition will be met by '3'.

Because 3 ⋅ 3 = 9 ≤ 10.

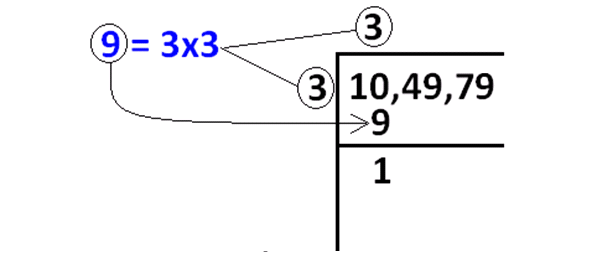
In the above picture, 9 is subtracted from 10 and we got the remainder 1.

Step 3 :

Now, we have to bring down 49 and quotient 3 to be multiplied by 2 as given in the picture below.

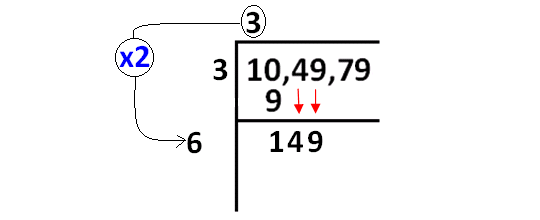
Step 4 :

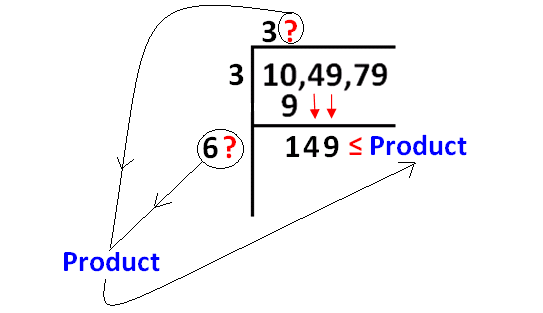
Now we have to take a same number at the two places indicated by '?'.

Then, we have to find the product as shown in the picture and also the product must meet the condition as indicated.

Step 5 :

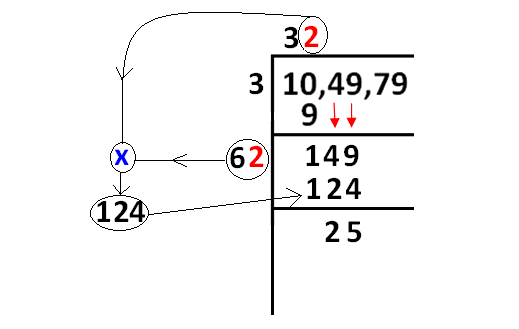
The condition said in step 4 will be met by replacing '?' with '2'.

Than we have to do the calculation as given in the picture.

Step 6 :

Now, we have to bring down 79 and quotient 32 to be multiplied by 2 as given in the picture below.

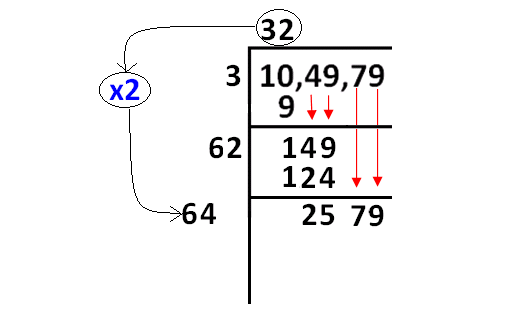
Step 7 :

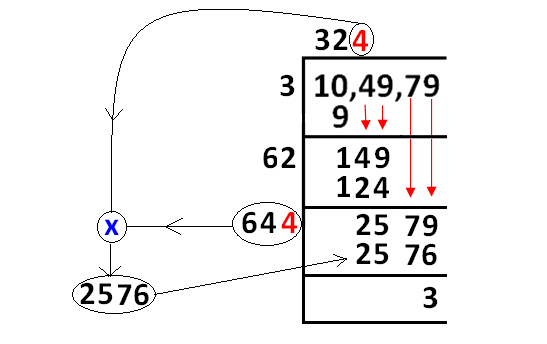
In finding square root of 104979 using long division, we obtain the remainder 3 and the quotient is 324.

324² = 104976 < 104979 ----(1)

The next perfect square number :

325² = 105625 > 104979 ----(2)

From (1) and (2),

324² < 104979 < 325²

Find the difference between 104979 and 325² :

325² - 104979 = 105625 - 104979

= 646

646 is the least number must be added to 104979 to get a perfect square.

Example 2 :

Find the least number which must be added to 1989 so as to get a perfect square.

Solution :

Find the square root of 1989 using long division method.

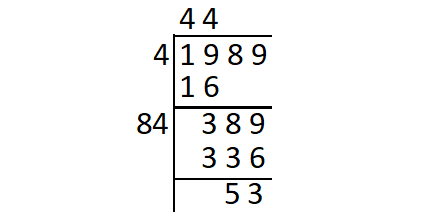
In finding square root of 1989 using long division, we obtain the remainder 53 and the quotient is 44.

44² = 1936 < 1989 ----(1)

The next perfect square number :

45² = 2025 > 1989 ----(2)

From (1) and (2),

44² < 1989 < 45²

Find the difference between 1989 and 45² :

45² - 1989 = 2025 - 1989

= 36

36 is the least number must be added to 1989 to get a perfect square.

Example 3 :

Find the least number which must be added  to 3250 so as to get a perfect square.

Solution :

Find the square root of 3250 using long division method.

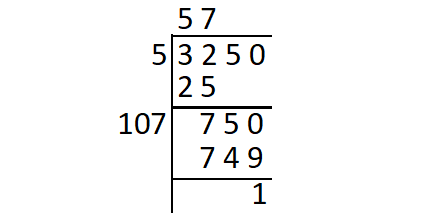
In finding square root of 3250 using long division, we obtain the remainder 1 and the quotient is 57.

57² = 3249 < 3250 ----(1)

The next perfect square number :

58² = 3364 > 3250 ----(2)

From (1) and (2),

57² < 3250 < 45²

57² < 3250 < 58²

Find the difference between 3250 and 58² :

58² - 3250 = 3364 - 3250

= 114

114 is the least number must be added to 3250 to get a perfect square.

Example 4 :

Find the least number which must be added to 4000 so as to get a perfect square.

Solution :

Find the square root of 4000 using long division method.

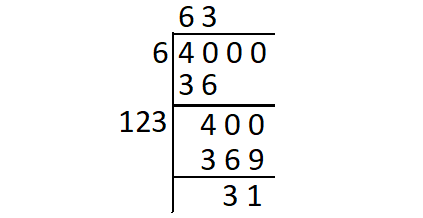
In finding square root of 4000 using long division, we obtain the remainder 31 and the quotient is 63.

63² = 3969 < 4000 ----(1)

The next perfect square number :

64² = 4096 > 4000 ----(2)

From (1) and (2),

63² < 4000 < 64²

Find the difference between 4000 and 64² :

64² - 4000 = 4096 - 4000

= 96

96 is the least number must be added to 4000 to get a perfect square.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.