FIND LENGTH OF THE ALTITUDE DRAWN FROM RIGHT ANGLE TO HYPOTENUSE

Property :

A perpendicular line drawn from the vertex of a right angled triangle divides the triangle into two triangles similar to each other and also to original triangle.

Let us see more results.

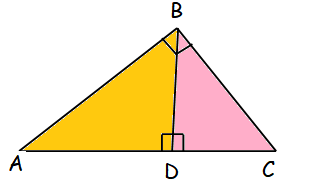
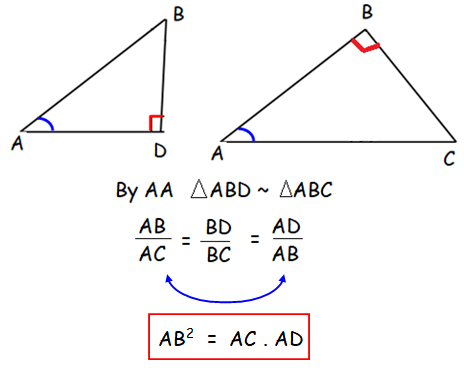
Result 1 :

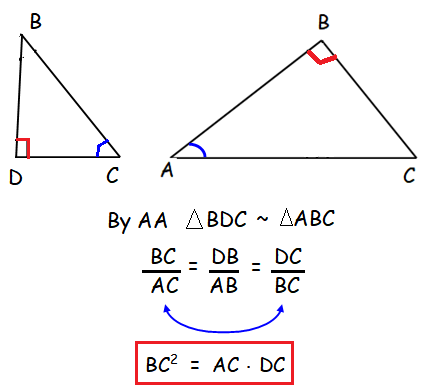
Result 2 :

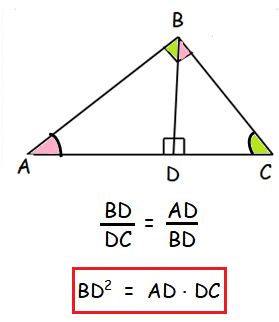
Result 3 :

Problem 1 :

Find x.

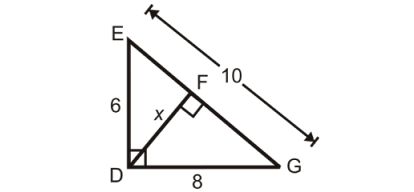
Solution :

EDG is a right triangle, EF is the perpendicular drawn from the right angle D.

ΔFDG, ΔEDF and ΔEDG are similar triangles to each other.

In triangles FDG and EDG.

<DFG  =  <GDE   (A)

<FGD  =  <EGD  (A)

ΔFDG ~ ΔEDG.

Using angle angle postulate, we prove that the triangles are similar. 

If two triangles are similar, then the ratio of corresponding sides will be equal.

In ΔFDG and ΔEDG :

DG/EG  =  DF/DE

8/10  =  x/6

x  =  48/10

x  =  4.8

So, the required length of x is 4.8.

Problem 2 :

Find x and y.

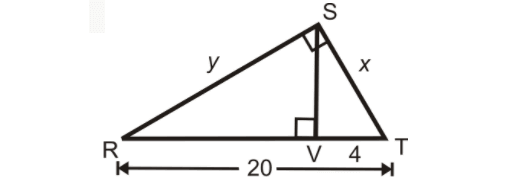
Solution :

From the results given above,

Problem 3 :

Find x.

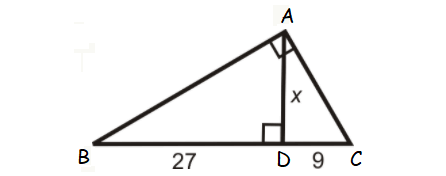
Solution :

AD² = BD ⋅ DC

x² = 27 ⋅ 9

x  =  √27(9)

x  =  9√3

So, the value of x is  9√3.

Problem 4 :

Find x and y.

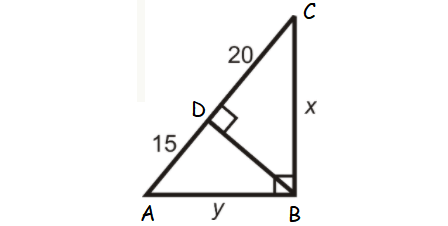
Solution :

AC  =  AD + DC

AC  =  15 + 20  ==>  35

BC²  =  DC ⋅ AC

x²  =  DC ⋅ AC

x²  =  20 ⋅ 35

x  =  √20 ⋅ 35

x  =  10√7

So, the value of x is 10√7.

Problem 5 :

Find y.

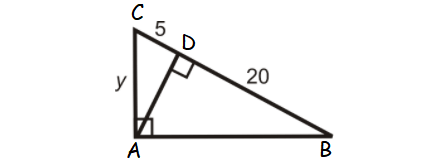
Solution :

BC  =  BD + DC

BC  =  20+5  ==>  25

AC²  =  CD ⋅ BC

AC  =  √(5 ⋅ 25)

AC  =  5√5

y  =  5√5

So, the value of y is 5√5.

Problem 6 :

Find x.

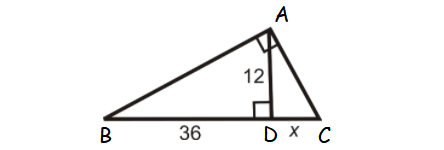
Solution :

AD²  =  BD ⋅ DC

12²  =  36 ⋅ x

144  =  36x

x  =  144/36

x  =  4

So, the value of x is 4.

Problem 7 :

Find z.

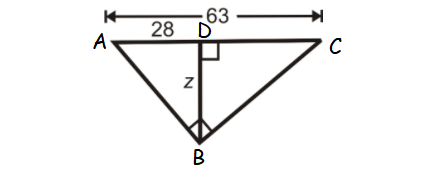
Solution :

AC  =  AD + DC

63  =  28 + DC

DC  =  35

AB²  =  AD ⋅ DC

z²  =  28 ⋅ 63

z  =   √(28 ⋅ 63)

z  =   42

So, the value of z is 42.

Problem 8 :

Find x, y and z.

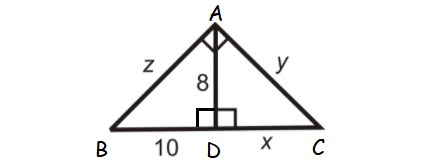
Solution :

In triangle ADB,

AB²  =  BD² + AD²

z²  =  10² + 8²

z²  =  164

z  =   √164

z  =  2 √41

AD²  =  BD ⋅ DC

8²  =  10 ⋅ x

x  =  64/10

x  =  6.4

AC²  =  AD² + DC²

y²  =  8² + (6.4)²

 y²  =  64 + 40.96

 y²  =  104.96

y  =  √104.96

y  =  10.24

So, the value of x is 6.4 and value of y is 10.24.

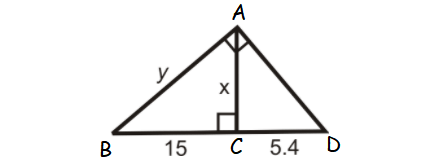
Problem 9 :

Find x and y.

Solution :

AC²  =  BC ⋅ CD

x²  =  15 (5.4)

x  =  √81

x  =  9

In triangle ABC,

AB²  =  BC²+AC²

y²  =  15²+9²

y²  =  225+81

y  =  √306

y  =  3√34

So, the value of x is 9 and value of y is 3√34.

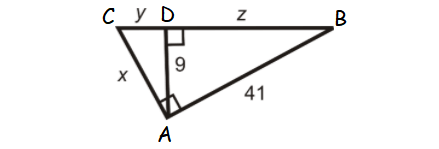
Problem 10 :

Find x, y and z.

Solution :

In triangle ADB,

AB²  =  AD² + DB²

41²  =  9² + DB²

1681-81  =  DB²

DB  =  √1600

z  =  40

AD²  =  CD ⋅ DB

9²  =  y ⋅ z

81  =  40y

y  =  81/40

y  =  2.025

In triangle ADC,

AC²  =  CD²+DA²

AC²  =  y²+9²

AC²  =  (2.025)²+9²

AC²  =  4.1+81

AC²  =  85.1

AC  =  √85.1

AC  =  9.2

x  =  9.2

So, the value of x is 9.2 and value of y is 2.205.

Problem 11 :

A roof has a cross section that is a right triangle. The diagram shows the approximate dimensions of this cross section. 

a. Identify the similar triangles.

b. Find the height h of the roof.

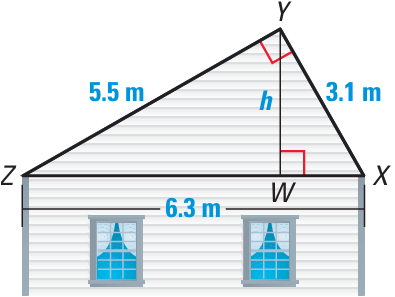
Considering triangles, ZYW and YZX.

∠YZW = ∠YZX (Common)

∠YWZ = ∠ZYX (90 degree)

YW/YX = ZY/ZX = ZW/ZY ------(1)

Using AA, the triangles ZYW and YZX are similar.

Considering triangles, ZWX and YZX.

∠YXW = ∠YXZ (Common)

∠YWX = ∠ZYX (90 degree)

YW/ZY = YX/ZX = WX/YX  --------(2)

(1) = (2)

ZW/ZY = WX/YX

From this, triangles ZYW and YWX are similar.

From (2),

YW/ZY = YX/ZX

h/5.5 = 3.1/6.3

h = (3.1/6.3) (5.5)

h = 2.7

So, the height of the roof is 2.7 meters.

Problem 12 :

To estimate the height of a monorail track, your friend holds a cardboard square at eye level. Your friend lines up the top edge of the square with the track and the bottom edge with the ground. You measure the distance from the ground to your friend’s eye and the distance from your friend to the track.

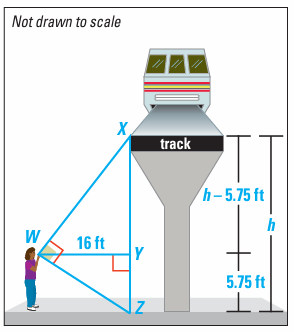
Solution :

In triangle WYZ and WXY.

∠XWY = ∠WZY

∠WYX = ∠WYZ

XY/WY = WY/YZ

(h-5.75) / 16 = 16 / 5.75

(h - 5.75)5.75 = 256

h - 5.75 = 256/575

h - 5.75 = 44.52

h = 44.52 + 5.75

h = 50.27

Approximately the height is 50 feet.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.