FIND THE MAXIMUM AND MINIMUM VALUE OF QUADRATIC FUNCTION

The graph of a quadratic function will always be a parabola which is either open upward or downward. 

General form of quadratic function is 

f(x) = ax² + bx + c

Maximum Value of a Quadratic Function

The quadratic function f(x) = ax² + bx + c will have only the maximum value when the the leading coefficient or the sign of 'a' is negative.

When 'a' is negative the graph of the quadratic function will be a parabola which opens down. 

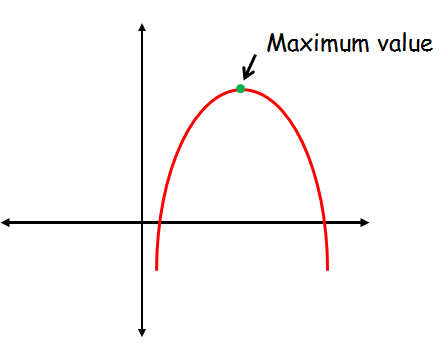
The maximum value is 'y' coordinate at the vertex of the parabola.  

Note :

There is no minimum value for the parabola which opens down. 

Minimum Value of a Quadratic Function

The quadratic function f(x) = ax² + bx + c will have only the minimum value when the the leading coefficient or the sign of 'a' is positive.

When 'a' is positive, the graph of the quadratic function will be a parabola which opens up. 

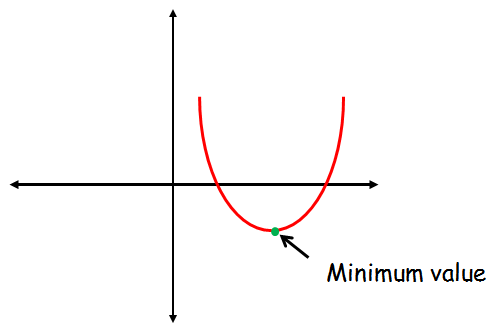
The minimum value is 'y' coordinate at the vertex of the parabola.  

Note :

There is no maximum value for the parabola which opens up.

Minimum or maximum value of the quadratic functions can be figured it out using any of the following ways.

i) Using formula

ii) writing in vertex form.

Find the minimum or maximum value of the quadratic function given below. 

Problem 1 :

f(x)  =  2x² + 7x + 5

Solution :

Because the coefficient of x² is positive, the parabola is open upward.

So, the function will have only the minimum value and the minimum value is y-coordinate of the vertex.  

To find the y-coordinate of the vertex, first we have to find the x-coordinate of the vertex. 

Formula to find x-coordinate of the vertex is

=  -b/2a

Substitute a  =  2 and b  =  7. 

=  -7 / 2(2)

=  -7/4

To find the y-coordinate of the vertex, substitute -7/4 for x in the given function.

y-coordinate is

=  f(-7/4)

=  2(-7/4)² + 7(-7/4) + 5

  =  2(49/16) - (49/4) + 5

  =  (49/8) - (49/4) + 5

  =  (49 - 98 + 40)/8

  =  -9/8

The minimum value is -9/8.

Problem 2 :

f(x)  =  -2x² + 6x + 12

Solution :

Because the coefficient of x² is negative, the parabola is open downward.

So, the function will have only the maximum value and the maximum value is y-coordinate of the vertex.  

To find the y-coordinate of the vertex, first we have to find the x-coordinate of the vertex. 

Formula to find x-coordinate of the vertex is

=  -b/2a

Substitute a = -2 and b = 6. 

=  -6/2(-2)

=  -6/(-4)

=  3/2

To find the y-coordinate of the vertex, substitute 3/2 for x in the given function.

y-coordinate is

=  f(3/2)

=  -2(3/2)² + 6(3/2) + 12

  =  -2(9/4) + 3(3) + 12

=  -9/2 + 9 + 12

  =  -9/2 + 21

=  (-9 + 42)/2

=  33/2

The maximum value is 33/2.

Problem 3 :

f(x) = -5x² + 30x + 200

Solution :

Because the coefficient of x² is negative, the parabola is open downward.

So, the function will have only the maximum value and the maximum value is y-coordinate of the vertex.  

To find the y-coordinate of the vertex, first we have to find the x-coordinate of the vertex. 

Formula to find x-coordinate of the vertex is

=  -b/2a

Substitute a = -5 and b = 30. 

=  -30/2(-5)

=  -30/(-10)

=  3

To find the y-coordinate of the vertex, substitute 3 for x in the given function.

y-coordinate is

=  f(3)

=  -5(3)² + 30(3) + 200

  =  -5(9) + 90 + 200

=  -45 + 290

  =  245

The maximum value is 245.

Problem 4 :

f(x) = 3x² + 4x + 3

Solution :

Because the coefficient of x² is positive, the parabola is open upward.

So, the function will have only the minimum value and the minimum value is y-coordinate of the vertex.  

To find the y-coordinate of the vertex, first we have to find the x-coordinate of the vertex. 

Formula to find x-coordinate of the vertex is

=  -b/2a

Substitute a = 3 and b = 4. 

=  -4/2(3)

=  -2/3

To find the y-coordinate of the vertex, substitute -2/3 for x in the given function.

y-coordinate is

=  f(-2/3)

=  3(-2/3)² + 4(-2/3) + 3

  =  3(4/9) - 8/3 + 3

  =  4/3 - 8/3 + 3

  =  (4 - 8)/3 + 3  

=  -4/3 + 3

=  -4/3 + 9/3

  =  (-4 + 9)/3

=  5/3

The minimum value is 5/3.

Problem 5 :

A flare is fired vertically from the top of a platform so that its height h, in meters after time t in seconds is given by

h(t) = 4 + 30y - 5y²

What is the maximum height that the flare reaches ?

Solution :

Given that, h(t) = 4 + 30y - 5y²

h(t) = - 5y² + 30y + 4

= -5[y² - 6y] + 4

= -5[y² - 2y(3) + 3² - 3²] + 4

= -5[(y - 3)² - 9] + 4

= -5(y - 3)² + 45 + 4

h(t) = -5(y - 3)² + 49

Comparing with y = a(x - h)² + k

Here vertex will be at (h, k), then (3, 49) is the vertex of the parabola.

Hence the maximum height reached by the flare is 49 meters in 3 seconds.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.