FIND MEDIAN LOWER QUARTILE AND UPPER QUARTILE PRACTICE PROBLEMS

Problem 1 :

The times spent (in minutes) by 24 people in a queue at a supermarket, waiting to be served at the checkout, were:

1.4, 5.2, 2.4, 2.8, 3.4, 3.8, 

2.2, 1.5, 0.8, 0.8, 3.9, 2.3, 4.5, 

1.4, 0.5, 0.1, 1.6, 4.8, 1.9, 0.2, 3.6,

5.2, 2.7, 3.0

a) Find the median waiting time and the upper and lower quartiles.

b) Find the range and interquartile range of the waiting time.

c) Complete the following statements:

i) “50% of the waiting times were greater than ......... minutes.”

ii) “75% of the waiting times were less than ...... minutes.”

iii) “The minimum waiting time was ........ minutes and the maximum waiting time was ..... minutes. The waiting times were spread over ...... minutes.”

Solution :

By writing the data set from least to greatest.

0.1, 0.2, 0.5, 0.8, 0.8, 1.4, 1.4, 1.5, 1.6, 1.9,

2.2, 2.3, 2.4, 2.7, 2.8, 3.0, 3.4,

3.6, 3.8, 3.9, 4.5, 4.8, 5.2, 5.2

(a)  Number of data values  =  24

Median(Q₂) =  (2.3+2.4)/2

Median  =  2.35

Note :

Since we don't find median value in the given data set, we divide the data set into two parts without ignoring the median.

0.1, 0.2, 0.5, 0.8, 0.8, 1.4, 1.4, 1.5, 1.6, 1.9, 2.2, 2.3

Median of lower half  =  (1.4+1.4)/2

Lower quartile(Q₁)  =  1.4

2.4, 2.7, 2.8, 3.0, 3.4, 3.6, 3.8, 3.9, 4.5, 4.8, 5.2, 5.2

Median of upper half  =  (3.6+3.8)/2

Upper quartile(Q₃)  =  3.7

(b)  Range  =  Large value - Small value

=  5.2-0.1

=  5.1

Interquartile range(IQR)  =  Q₃ - Q₁

=  3.7-1.4

=  2.3

(c)

i) 3.25

ii) 3.7

iii) The minimum waiting time was 0.1 minutes and the maximum waiting time was 5.2 minutes. The waiting times were spread over 5.1 minutes.”

Problem 2 :

For each of the following data sets, make sure the data is ordered and then find :

i) the median

ii) the upper and lower quartiles

iii) the range

iv) the interquartile range.

5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 11, 11, 11, 12, 12

Solution :

5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 11, 11, 11, 12, 12

(i)  The given data is already arranged. 

Number of data values  =  23

Median(Q₂) =  (23+1)/2 ^th value

=  12^th value

Median  =  9

(ii)

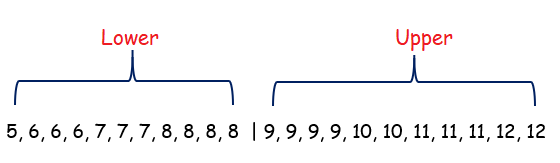
By ignoring the median, we will divide the entire data set into two parts.

Lower quartile :

5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 8,

Middle value of lower half  =  7

Lower quartile(Q₁)  =  7

Upper quartile :

9, 9, 9, 9, 10, 10, 11, 11, 11, 12, 12

Middle value of upper half  =  10

Upper quartile(Q₃)  =  10

(iii)  Range  =  Large value - small value

=  12-5

=  7

So, range is 7.

(iv)   Interquartile range :

IQR  =  10-7

IQR  =  3

Example 2 :

11, 13, 16, 13, 25, 19, 20, 19, 19, 16, 17, 21, 22, 18, 19, 17, 23, 15

Solution :

By arranging the data values from least to greatest.

11, 13, 13, 15, 16, 16, 17, 17, 18, 19, 19, 19, 19, 20, 21, 22, 23, 25

(i)  Number of data values  =  18

Median  =  (9^th value + 10^th value)/2

=  (18+19)/2

=  18.5

Median(Q₂)  =  18.5

Note :

Since we don't find median value in the given data set, we divide the data set into two parts without ignoring the median.

(ii)

Lower :  

11, 13, 13, 15, 16, 16, 17, 17, 18

Middle value of lower half  =  16

Lower quartile(Q₁)  =  16

Upper :  

19, 19, 19, 19, 20, 21, 22, 23, 25

Middle value of upper half  =  20

Upper quartile(Q₃)  =  20

(iii)  Range 

Range  =  Large value - small value

=  25-11

=  14

So, range is 14.

(iv)   Interquartile range :

IQR  =  20-16

IQR  =  4

Problem 3 :

23.8, 24.4, 25.5, 25.5, 26.6, 26.9, 27, 27.3, 28.1, 28.4, 31.5

Solution :

It is already arranged.

23.8, 24.4, 25.5, 25.5, 26.6, 26.9, 27, 27.3, 28.1, 28.4, 31.5

(i)  Number of data values  =  11

Median  =  (11+1)/2

=  6^th value

Median(Q₂)  =  26.9

(ii)

Lower :  

23.8, 24.4, 25.5, 25.5, 26.6

Middle value of lower half  =  25.5

Lower quartile(Q₁)  =  25.5

Upper :  

 27, 27.3, 28.1, 28.4, 31.5

Middle value of upper half  =  28.1

Upper quartile(Q₃)  =  28.1

(iii)  Range :

=  Large value - small value

=  31.5 - 23.8

=  7.7

So, range is 7.7.

(iv)   Interquartile range :

IQR  =  28.1-25.5

IQR  =  2.6

Problem 4 :

The box plot below shows the weights of a group of dogs.

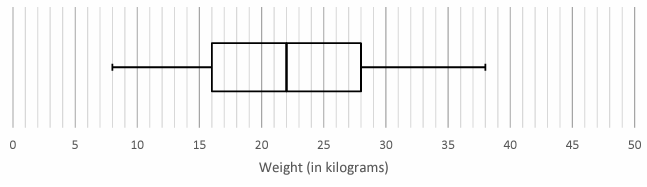
a) What is the weight of the lightest dog in the group?

(b) What is the median weight?

(c) What is the weight of the heaviest dog in the group?

(d) What is the range of the weights?

(e) What is the interquartile range of the weights?

Solution :

a) The weight of the lightest dog is 8 kg.

b)  The median weight is 2 kg.

c)  The heaviest dog is 38 kg

d) Range = weight of heaviest dog - weight of lightest dog

= 38 - 2

= 36 kg

e) Interquartile range = Q₃ - Q₁

= 28 - 16

= 12

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.