FIND THE MISSING SIDE LENGTH USING BASIC PROPORTIONALITY THEOREM

Question 1 :

In the figure given below the sides DE and BC are parallel. Find the length of the side EC ?

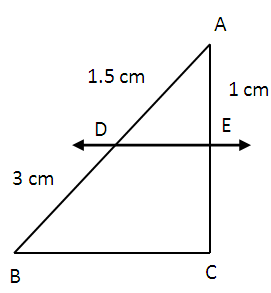
Solution :

Let EC = x.

Given that :

The sides DE and BC are parallel.

By using basic proportionality theorem, we have 

AD/DB  =  AE/EC  ----(1)

AD  =  1.5 cm,  DB  =  3 cm,  AE  =  1 cm 

By applying the known values in (1), we get

1.5/3  =  1/x

 1.5x  =  3

x  =  3/1.5

x  =  2 cm

Hence, the length of side EC is 2 cm.

Question 2 :

In the figure given below the sides DE and BC are parallel. Find the length of the side AD ?

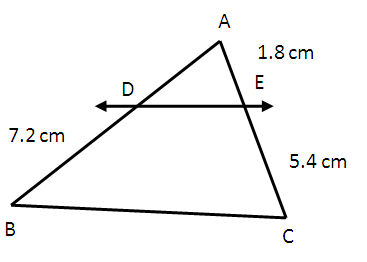
Solution :

Let AD = x.

Given that :

The sides DE and BC are parallel.

By using basic proportionality theorem, we have 

AD/DB  =  AE/EC  ----(1)

AD  =  x  DB  =  7.2 cm   AE  =  1.8 cm  EC  =  5.4 cm

x/7.2  =  1.8/5.4

 5.4 x  =  1.8 x 7.2

x  =  (1.8 x 7.2)/5.4

x  =  2.4 cm

Question 3 :

E and F are points on the sides PQ and PR respectively of a ∆ PQR. For each of the following cases, state whether EF  ∥ QR.

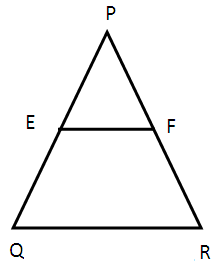
(i)  PE  =  3.9 cm, EQ  =  3 cm, PF  =  3.6 cm and FR  =  2.4 cm

(ii) PE  =  4 cm, EQ  =  4.5 cm, PF  =  8 cm and FR  =  9 cm

(iii) PQ  =  1.28 cm PR  =  2.56 cm PE  =  0.18 cm and  PF  =  0.36 cm

Solution :

Given that :

PE  =  3.9 cm , EQ  =  3 cm, PF  =  3.6 cm and FR  =  2.4 cm

PE/EQ  =  PF/FR ----(1)

3.9/3  =  3.6/2.4

 1.3  ≠  1.5

So, the sides EF and QR are not parallel.

(ii) PE = 4 cm , EQ = 4.5 cm, PF = 8 cm and FR = 9 cm

Solution :

According to basic proportionality theorem, we have

PE/EQ = PF/FR

4/4.5 = 8/9

0.88 = 0.88

So, the sides EF and QR are parallel.

(iii)  PQ = 1.28 cm PR = 2.56 cm PE = 0.18 cm and  PF = 0.36 cm

Solution :

PQ  =  PE + EQ

1.28  =  0.18 + EQ

EQ  =  1.28 - 0.18  =  1.1

PR  =  PF + FR

2.56  =  0.36 + FR 

2.56 - 0.36  =  FR

FR  =  2.2

According to basic proportionality theorem, we have

PE/EQ = PF/FR

0.18/1.1 = 0.36/2.2

 0.1636 = 0.1636

So, EF is parallel to QR.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.