FIND THE MISSING SIDE USING TRIGONOMETRIC RATIOS

Consider a right-angled triangle, right-angled at B.

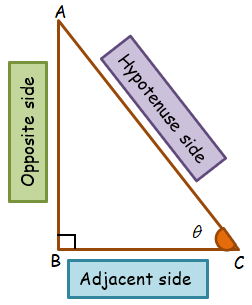
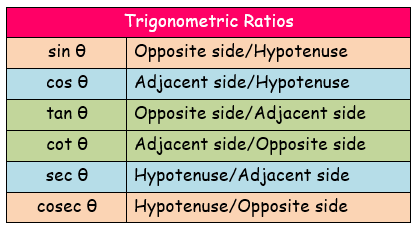
The trigonometry ratios for a specific angle θ. There are six trigonometric ratios. 

Find the value of x, giving your answer correct to 2 decimal places :

Example 1 :

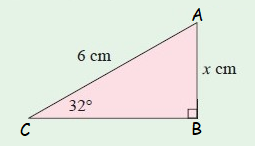
Solution :

In the figure,

Opposite side (AB)  =  x cm

Hypotenuse (AC)  =  6 cm

Here θ  =  32˚

The sides opposite and hypotenuse are involving in the trigonometric ratio sin θ

sin θ  =  Opposite side/Hypotenuse  =  AB/AC

sin 32˚  =  x/6

By using the calculator, we get

0.529  =  x/6

(0.53 × 6)  =  x

x  =  3.18

So, the value of x is 3.18 cm

Example 2 :

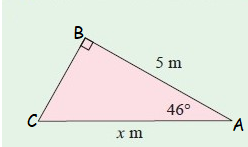
Solution :

In the figure,

Hypotenuse side AC  =  x cm

Adjacent side AB  =  5 cm

Here θ  =  46˚

The sides hypotenuse and adjacent are involving in the trigonometric ratio sec θ

sec 46˚  =  Hypotenuse/Adjacent side  =  AC/AB

sec 46˚  =  x/5

By using the calculator, we get

1.44  =  x/5

(1.44 × 5)  =  x

x  =  7.2

So, the value of x is 7.20 cm

Example 3 :

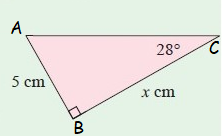
Solution :

In the figure,

Opposite side AB  =  5 cm

Adjacent side BC  =  x cm

Here θ  =  28˚

The sides opposite and adjacent are involving in the trigonometric ratio tan θ

tan 28˚  =  Opposite side/Adjacent side  =  AB/BC

tan 28˚  =  5/x

By using the calculator, we get

0.532  =  5/x

x  =  5/0.532

x  =  9.4

So, the value of x is 9.40 cm

Find, to 2 significant figures, the value of θ :

Example 4 :

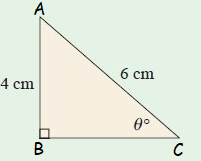
Solution :

In the figure,

Opposite side AB  =  4 cm

Hypotenuse side AC  =  6 cm

Here θ  =  θ˚

The sides opposite and hypotenuse are involving in the trigonometric ratio sin θ

sin θ  =  Opposite side/Hypotenuse side  =  AB/AC

sin θ˚  =  4/6

sin θ˚  =  2/3

 θ˚  =  sin^-1(2/3)

By using the calculator, we get

θ  =  42˚

So, the value of θ is 42˚

Example 5  :

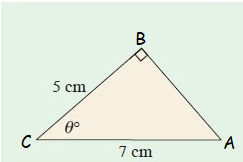
Solution :

In the figure,

Hypotenuse side AC  =  7 cm

Adjacent side BC  =  5 cm

Here θ  =  θ˚

The sides hypotenuse and adjacent are involving in the trigonometric ratio sec θ

sec θ˚  =  Hypotenuse/Adjacent side  =  AC/BC

sec θ˚  =  7/5

θ˚  =  sec^-1 (7/5)

By using the calculator, we get

θ  =  44˚

So, the value of θ is 44˚

Example 6 :

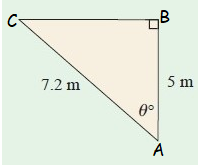
Solution :

In the figure,

Hypotenuse side AC  =  7.2 cm

Adjacent side AB  =  5 cm

Here θ  =  θ˚

The sides hypotenuse and adjacent are involving in the trigonometric ratio sec θ

sec θ˚  =  Hypotenuse/Adjacent side  =  AC/AB

sec θ˚  =  7.2/5

θ˚  =  sec^-1 (7.2/5)

By using the calculator, we get

θ  =  46˚

So, the value of θ is 46˚

Example 7 :

A guy wire is attached to a telephone pole 8 meter above the ground and it makes an angle of 50 degree with the ground. How long is the wire ?

Solution :

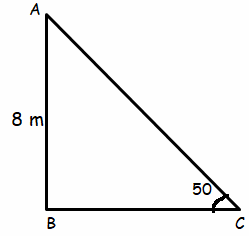
Length of wire = AC

sin θ = opposite side / hypotenuse

sin 50 = AB/AC

0.766 = 8/AC

AC = 8/0.766

AC = 10.44 m

So, the length of the wire is 10.4 m.

Example 8 :

When a child flying a kite has let out 50 m of string, the string makes an angle of 55 degree with the ground. How high is the kite ?

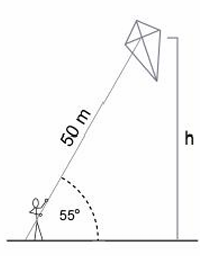
Solution :

Length of wire = 50 m

sin θ = opposite side / hypotenuse

sin 55 = h/50

h = 50(sin 55)

= 50(0.819)

= 40.95

So, the required height is 41 m.

Example 9 :

From P, the top of the building <APC and <BPC are measured as shown. The length of QB is 35 m, calculate AB, the height of building ?

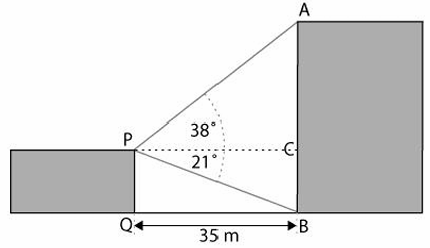
Solution :

In triangle APC,

tan θ = opposite side / adjacent side

tan 38 = AC/PC

0.7812 = AC/35

AC = 0.7812(35)

AC = 27.34

Since PC and QB are parallel,

<BPC = <PBQ

tan 21 = PQ/QB

0.383 = PQ/35

PQ = 0.383(35)

= 13.40

PQ = BC = 13.4

AB = AC + BC

= 27.34 + 13.4

= 40.74 m

So, the height of the building is 40.7 m.

Example 9 :

Given <ACB = 48, <D = 31 and AD = 56 cm find the length of AC.

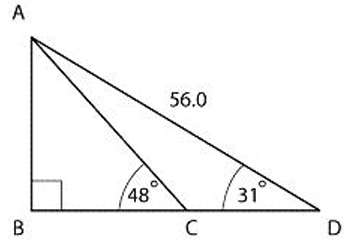
Solution :

In triangle ABD,

sin θ = opposite side / hypotenuse

sin 31 = AB/AD

0.515 = AB/56

AB = 0.515(56)

= 28.84

sin 48 = AB/AC

Applying the value of AB, we get

sin 48 = 28.84 / AC

AC = 28.84/sin 48

= 28.84/0.743

= 38.8

So, the length of AC is 38.8 cm.

Example 10 :

Calculate the area of the following plot of the land

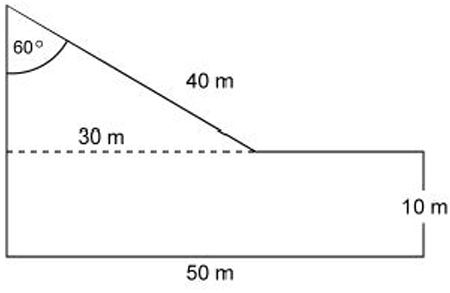
Solution :

In the triangle above,

base of the triangle = 30 m

height of the triangle = h

tan 60 = opposite side / adjacent side

√3 = opposite side / 30

opposite side = 30(√3)

= 30 (1.732)

= 51.96

Approximately 52 cm.

Area of triangle = (1/2) x base x height

= (1/2) x 30 x 52

= 15 x 52

= 1560

Area of rectangle = length x width

= 50 x 10

= 500

Total area = 1560 + 500

= 2060 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.