FIND THE MISSING SIDES AND ANGLES USING SIN LAW

The sine law is a relationship between the sides and angles in any triangle.

Let ABC be any triangle, where a, b, and c represent the measures of the sides opposite to the angle measures ∠A, ∠B, and ∠C, respectively. 

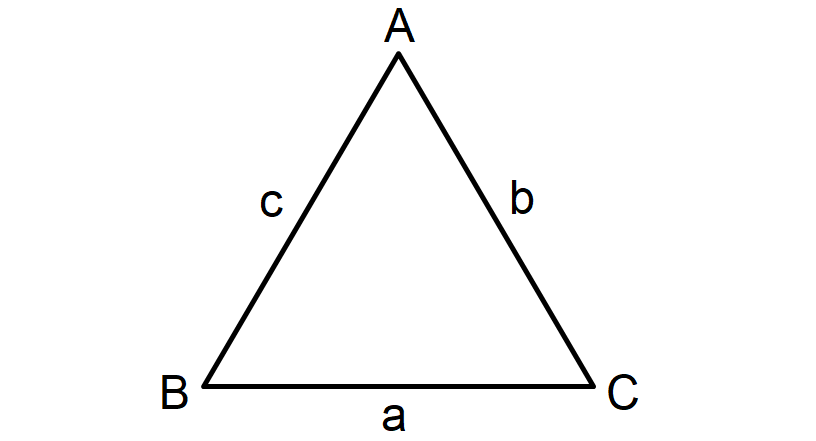
Then,

a/sin A  =  b/sin B  =  c/sin C

(or)

sin A/a  =  sin B/b  =  sin C/c

Examples

Example 1 :

Determine the value of the marked unknown angle in each.

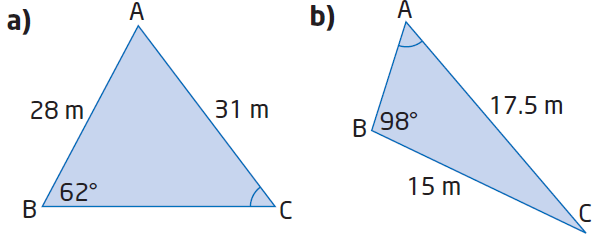
Solution :

(a)  From the picture given above, we know that we need to find the angle C.

BC  =  a, AC  =  b =  31 m and AB  =  c = 28 m

<B  =  62

a/sin A  =  b/sin B  =  c/sin C

31/sin 62  =  28/sin C

31/0.8829  =  28/sin C

35.11  =  28/sin C

sin C  =  28/35.11

sin C  =  0.7974

C  =  52.88°

Hence the required angle is 53° (approximately).

(b)  BC  =  a = 15, AC  =  b =  17.5 m and AB  =  c

<B  =  98, <A  =  ?

a/sin A  =  b/sin B  =  c/sin C

15/sin A  =  17.5/sin 98

15/sin A =  17.5/0.9902

15/sin A =  17.67

sin A  =  15/17.67

sin A  =  0.8488

Hence the required angle is 58° (approximately).

Example 2 :

Determining the lengths of all three sides and the measures of all three angles is called solving a triangle. Solve each triangle

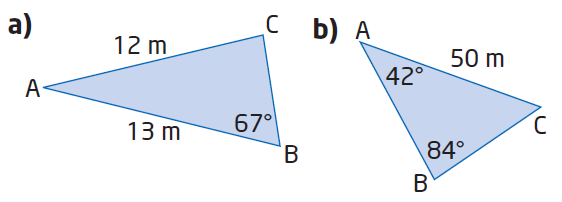
Solution :

(a)  AB = c = 13 m, BC = a, AC = b = 12 m

<B  =  67

a/sin A  =  b/sin B  =  c/sin C  ----(1)

a/sin A  =  12/sin 67  =  13/sin C

12/sin 67  =  13/sin C

12/0.9205  =  13/sin C

13.03  =  13/sin C

sin C  =  13/13.03

sin C  =  0.9976

<C  =  86

In triangle ABC,

<A + <B + <C  =  180

<A + 67 + 86  =  180

<A + 153  =  180

<A  =  180 - 153

<A  =  27

a/sin 27  =  12/sin 67  =  13/sin 86

a/sin 27  =  12/sin 67

a/0.4539  =  13.03

a  =  13.03(0.4539)

a  =  5.91 approximately 6 m

Hence the missing side and missing angles are 6 m and 86 respectively.

(b)  AB = c, BC = a, AC = b = 50 m

<A  =  42, <B  =  84

a/sin A  =  b/sin B  =  c/sin C

a/sin 42  =  50/sin 84  =  c/sin C

a/sin 42  =  50/sin 84 

a/0.6691  =  50/0.9945

a  =  50.27 (0.6691)

a  =  33.63 approximately 33.6 m

In triangle ABC,

<A + <B + <C  =  180

42 + 84 + <C  =  180

<C  =  180 - 126

<C  =  54

So, the missing side and missing angle are 33.6 m and 54 degree.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.