FIND THE QUOTIENT AND REMAINDER OF POLYNOMIALS USING LONG DIVISION

Find the quotient and remainder of the following.

Example 1 :

(10 + 7x + x²) ÷ (x + 2)

Solution :

Let us first write the degree of each polynomial in descending order.

Given, (10 + 7x + x²) ÷ (x + 2)

 (x² + 7x + 10) ÷ (x + 2)

Step 1 :

In the first step, we are going to divide the first term x² of the dividend by the first term x of the divisor.

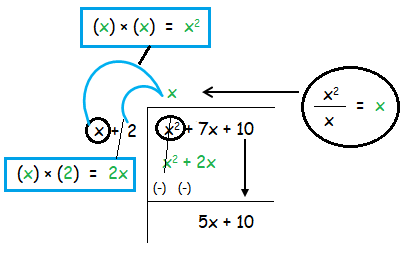
After changing the signs, +x² and -x² will get canceled. By simplifying, we get 5x + 10.

Step 2 :

In the second step again we are going to divide the first term that is 5x by the first term of divisor that is x.

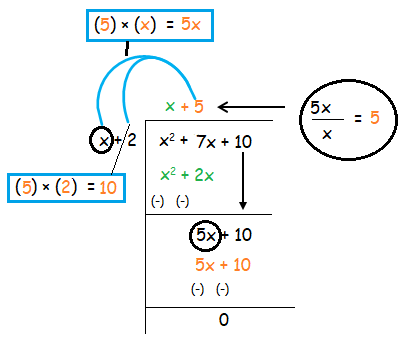
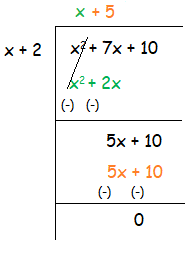
Quotient  =  x + 5

Remainder  =  0

Example 2 :

(3x³ + 11x² + 9x - 5) ÷ (x + 2)

Solution :

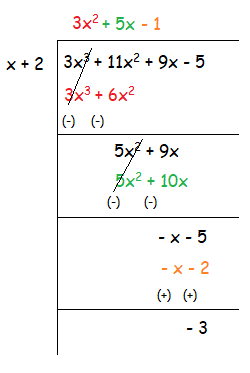
Quotient  =  3x² + 5x - 1

Remainder  =  - 3

Example 3 :

(x² - 25) ÷ (x + 5)

Solution :

The degree of the given polynomial is 2. But here we don't have x term, so we have to replace it by 0.

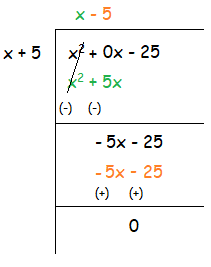
Quotient  =  x - 5

Remainder  =  0

Example 4 :

(x² - 1000) ÷ (x - 100)

Solution :

The degree of the given polynomial is 2. But here we don't have x term, so we have to replace it by 0.

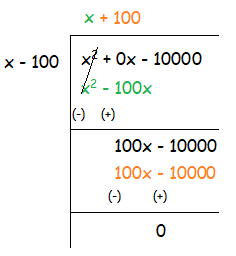
Quotient  =  x + 100

Remainder  =  0

Example 5 :

(30x³ + 50x) ÷ 5x

Solution :

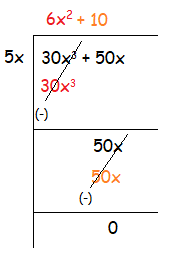
Quotient  =  6x² + 10

Remainder  =  0

Example 6 :

Find a and b if the polynomial x⁵ - ax + b is divisible by   x² - 4

Solution :

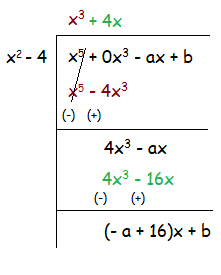
Quotient  =  x³ + 4x

Remainder  =  (-a + 16)x + b

Since it is given that x⁵ - ax + b is exactly divisible by  x² - 4, therefore remainder must be equal to zero.

That is,

(-a + 16)x + b  =  0

By comparing coefficients,

(-a + 16)x + b  =  0 . x + 0

- a + 16  =  0, b  =  0

- a  =  - 16, b  =  0

a  =  16 and b  =  0

So, a  =  16 and b  =  0

Example 7 :

The volume of a rectangular solid is given by the polynomial 3x⁴ - 3x³ - 33x² + 54x. The length of the solid is given by 3x and the width is given by x - 2. Find the height of the solid.

Solution :

Given,

Volume of a rectangular solid  =   3x⁴ - 3x³ - 33x² + 54x

Length of the solid  =  3x

Width of the solid  =  x - 2

Find the height of the solid.

Formula for Volume of a rectangle,

Volume of a rectangle  =  Length × Height × Width

3x⁴ - 3x³ - 33x² + 54x  =  (3x) × Height × (x - 2)

3x⁴ - 3x³ - 33x² + 54x  =  3x² - 6x × Height

Dividing by 3 on both sides,

x⁴ - x³ - 11x² + 18x  =  x² - 2x × Height

(x⁴ - x³ - 11x² + 18x) ÷ x² - 2x  =  Height

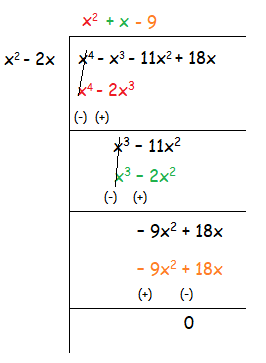
Quotient  =  x² + x - 9

Remainder  =  0

So, the height of the solid is x² + x - 9

Example 8 :

The area of a rectangle is given by 3x³ + 14x² - 23x + 6. The width of the rectangle is given by x + 6. Find an expression for the length of the rectangle.

Solution :

Given,

Area of a rectangle  =  3x³ + 14x² - 23x + 6

Width of the rectangle  =  x + 6

Find the length of the rectangle.

Formula for Area of a rectangle,

 Area of a rectangle  =  Length × Width

3x³ + 14x² - 23x + 6  =  Length × x + 6

(3x³ + 14x² - 23x + 6) ÷ x + 6  =  Length

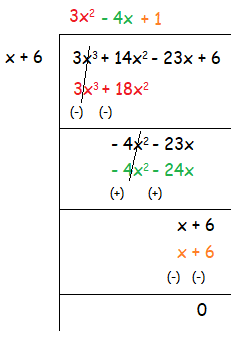
Quotient  =  3x² - 4x + 1

Remainder  =  0

So, the length of the rectangle is 3x² - 4x + 1

Example 9 :

Jordan is divided the polynomial x⁴ + x - 6 into the polynomial p(x) yesterday. Today his work is smudged and he cannot read p(x) or most of his answer . The only part he could read was the remainder x + 4. His teacher wants to find p(-3), what is p(-3)?

Solution :

Let p(x) = x⁴ + x - 6

To find the value of p(-3), without using long division also we can find the remainder.

p(-3) = (-3)⁴ + (-3) - 6

= 81 - 3 - 6

= 81 - 9

= 72

So, the remainder or the value of p(-3) is 72.

Example 10 :

Determine the value of 𝑘 such that when 𝑃(𝑥) = 𝑘𝑥³ + 5𝑥² − 2𝑥 + 3 is divided by 𝑥 + 1, the remainder is 7.

Solution :

𝑃(𝑥) = 𝑘𝑥³ + 5𝑥² − 2𝑥 + 3

x + 1 = 0

x = -1

While dividing the given polynomial p(x), we get the remainder 7.

𝑃(-1) = 𝑘(-1)³ + 5(-1)² − 2(-1) + 3

7 = k(-1) + 5(1) + 2 + 3

7 = -k + 5 + 2 + 3

7 = -k + 10

k = 10 - 7

k = 3

So, the value of k is 3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.