FIND THE RULE WHICH GIVES THE NUMBER OF MATCHSTICKS

Example 1 :

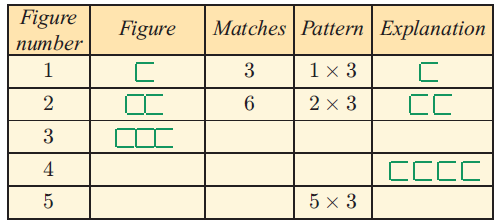
(a)  Complete a table for the first four figures in the pattern:

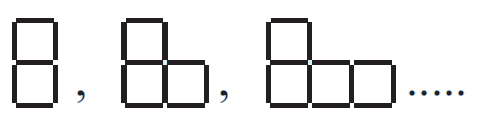
(b)  Find how many matches are required to make the:

i)  10^th figure      ii) 50^th figure

(c) Write a description of the pattern in words.

(d) Predict a general rule for finding the number of matches M in the n^th figure

Solution :

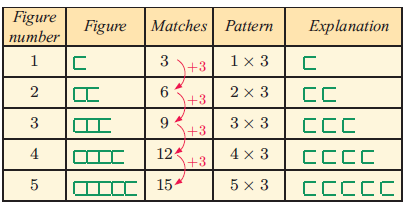
(a)

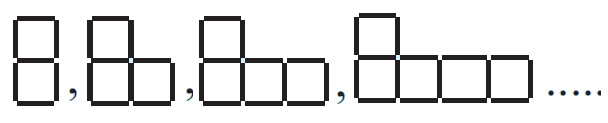
(b)  Number of match sticks in the 1^st picture  =  7

Number of match sticks in the 2^nd picture  =  10

Number of match sticks in the 3^rd picture  =  13

7, 10, 13, .............

To get the next term, we add 3 by the preceding term.

General term  =  3n+4

(i)  10^th term  =  3(10)+4  ==>  34

(ii)  50^th term  =  3(50)+4  ==>  154

(c)  To get the number of match sticks in each figure,  we use number times 3 plus 4.

(d) General rule  =  3n+4

Example 2 :

Consider the pattern:

(a)  Draw the next two figures and hence complete:

b) Find how many matches would be required to make the:

(i) 6^th figure  (ii) 20^th figure.

c)  Copy and complete:

“The number of matches is the figure number ......”.

d) Write a general rule for determining the number of matches M in the nth figure

Solution :

b) (i) 6^th figure (ii) 20^th figure.

General formula  =  3n

If n = 6, then 3n  ==>  3(6)  == > 18

If n = 20, then 3n  ==>  3(20)  == > 60

c)  “The number of matches is the figure number

times 3

d) M  =  3n

Example 3 :

a) Draw the next two section type fences.

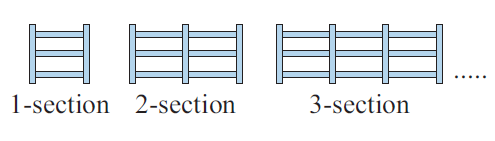
b)  If S is the number of steel lengths Wiktor requires to make an n - section fence, copy and complete the following table

c) Determine the formula which connects S and n.

d)  If Victor has an order for a 44-section fence, how many lengths of steel are required to make it?

Solution :

(a)

(b)  

5, 9, 13, .................

every time 4 is added.

c)  S - number of lengths and n - number of section

S  =  4n+1

d)  Number of lengths of steel are required 

S₄₄  =  4(44) + 1

=  176+1

=  177

So, 177 steels are needed.

Example 4 :

Builder Ben is experimenting with toothpicks to investigate housing designs:

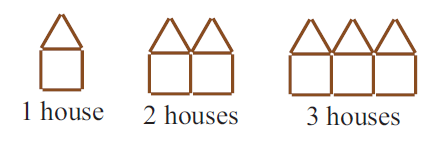
(a)   Draw toothpick diagrams for 4 houses and 5 houses.

(b)  If T is the number of toothpicks required to make h houses and complete the table.

(c)  Find the formula which connects T and h.

(d)  If Ben wanted to build 25 houses in a row, how many tooth picks would he need ?

Solution :

(a)  

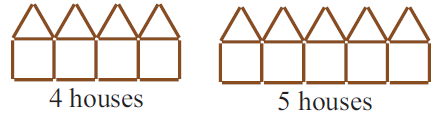
(b)  

(c)  By writing number of toothpicks required as sequence, we get

6, 11, 16, 21, ................

Every time 5 is added.

So, T  =  5h + 1

T-number of toothpicks and h - houses

(d)  If h  =  25

T  =  5(25) + 1

T  =  125+1

T  =  126

So, the number of toothpicks required to make 25th house is 126.

Example 5 :

Consider the pattern:

a) Copy and complete the table of values:

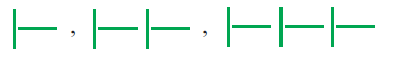
b) Write a rule linking n and M.

Solution :

(a)  Number of matchsticks used in 1^st picture  =  2

Number of matchsticks used in 2^nd picture  =  4

Number of matchsticks used in 3^rd picture  =  6

using this pattern we can fill up

(b)  Number of matches(M)  =  2n

Example 6 :

Consider the pattern:

a) Copy and complete the table of values :

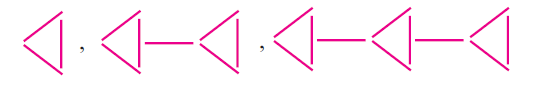
b) Write a rule linking n and M.

Solution :

(a)  Number of matchsticks used in 1^st picture  =  3

Number of matchsticks used in 2^nd picture  =  7

Number of matchsticks used in 3^rd picture  =  11

By observing this, we notice every time 4 is added.

(b)  Number of matches (M)  =  4n - 1

Example 7 :

The following diamond pattern has dots marked where the diamond cross.

a) Complete the table.

b)  Use the table of values to find the rule linking the number of dots D with the number of diamonds n.

c) Use the rule to find the number of dots if there are 32 diamonds.

Solution :

Let n be the number of diamonds and D be the number of dots.

• When n = 1, D = 0
• When n = 2, D = 2
• When n = 3, D = 4
• When n = 4, D = 6
• When n = 5, D = 8

b)  Rule :

D = 2n - 2

c) Number of dots when 32 diamonds are there.

D = 2(32) - 2

D = 64 - 2

D = 62

So, 62 dots will be there, when we have 32 diamonds.

Example 8 :

Find the output number if the input number 27 and the rule is "one third the number minus two"

Solution :

Let x be the input and y be the output.

y = (1/3) of x - 2

y = (x/3) - 2

When x = 27

y = (27/3) - 2

= 9 - 2

= 7

When input is 27, the output is 7.

Example 9 :

Here is a sequence of patterns.

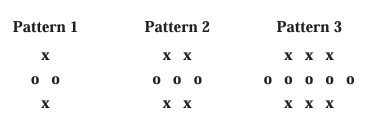
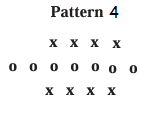
a)  Draw pattern 4

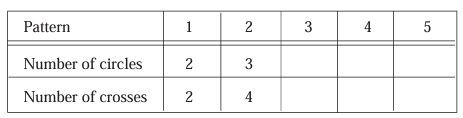
b)  Copy and complete the following table.

c) What pattern do you notice in the number of crosses row in the table ?

d)  How many circles are there in pattern 20 ?

Solution :

a) In pattern 4

b)

c) From the table, the number of crosses is multiples of 2.

d)  In pattern 20, there must be 40 crosses will be there. Then number of circles in it will be 39.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.