FIND THE SEQUENCE WITH THE GIVEN WITH GIVEN RULE

Use the rules to list the first six terms of the sequence :

Example 1 :

Start with 1 and add 2 each time

Solution :

Hence, the first six terms of the sequence are 

1, 3, 5, 7, 9, 11, ........

Example 2 :

Start with 3 and multiply by 2 each time

Solution :

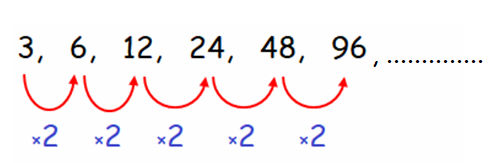
Hence, the first six terms of the sequence are

3, 6, 12, 24, 48, 96, ................

Example 3 :

Start with 24 and subtract 8 each time

Solution :

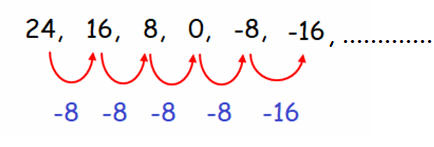
Hence, the first six terms of the sequence are

24, 16, 8, 0, -8, -16, ...............

Example 4 :

Start with 32 and divide by 2 each time

Solution :

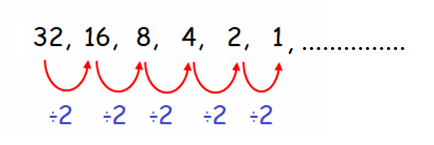
Hence, the first six terms of the sequence are

32, 16, 8, 4, 2, 1, ..........

Example 5 :

start with 5 and double each time

Solution :

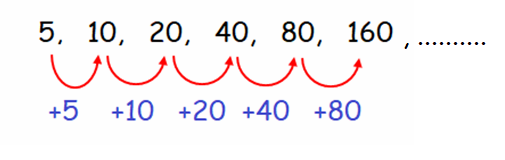
Hence, the first six terms of the sequence are

5, 10, 20, 40, 80, 160, .........

Example 6 :

Start with 1 and 2 and add the previous two numbers to get the next one.

Solution :

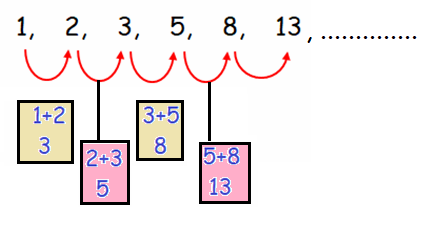
Hence, the first six terms of the sequence are

1, 2, 3, 5, 8, 13, .............

Example 7 :

For the sequence 

6, 12, 24, 48, 96, ............

a) Calculate the next 2 terms of the sequence.

b)  Determine the general formula for nth term.

Solution :

6, 12, 24, 48, 96, ............

By observing the sequence, we know that to get the next term we have to multiply the preceding term by 2

a) 6^th term

= 96 (2)

= 192

7th term :

= 192 (2)

= 384

So, the next two terms are 192 and 384.

b)  General formula 

t_n = ar^(n-1)

a = 6, r = 2

t_n= 6(2)^n-1

Example 8 :

Calculate the next three terms of the sequence.

1, 4, 16, 64, 256

i) Determine the formula for the nth term of the sequence.

Solution :

By observing the sequence, each number is a perfect square. These are perfect squares of multiples of 4.

i) Next three terms will be :

1², 2², 4², 8², 16², 32², 64², 128², ........

1, 4, 16, 64, 256, 1024, 4096, 16384, .............

General term :

(2^{n - 1})²

Example 9 :

Determine the formula for the general term of each of the following sequences :

i)  15, 75, 375, 1875, 9375,.............

ii)  1, 3, 9, 27, 81, ............

iii)  20, 200, 2000, 20000, .........

iv)  4, 28, 196, 1372, 9604, .............

Solution :

i)  15, 75, 375, 1875, 9375,.............

General term :

Dividing each term by the preceding term, we get 5. So, the given sequence is geometric sequence.

First term (a) = 15, common ratio (r) = 5

tn = ar^{n - 1}

= 15(5)^{n - 1}

ii)  1, 3, 9, 27, 81, ............

General term :

Dividing each term by the preceding term, we get 3. So, the given sequence is geometric sequence.

First term (a) = 1, common ratio (r) = 3

tn = ar^{n - 1}

= 1(3)^{n - 1}

iii)  20, 200, 2000, 20000, .........

General term :

Dividing each term by the preceding term, we get 10. So, the given sequence is geometric sequence.

First term (a) = 20, common ratio (r) = 10

tn = ar^{n - 1}

= 20(10)^{n - 1}

iv)  4, 28, 196, 1372, 9604, .............

General term :

Dividing each term by the preceding term, we get 7. So, the given sequence is geometric sequence.

First term (a) = 4, common ratio (r) = 7

tn = ar^{n - 1}

= 4(7)^{n - 1}

Example 10 :

A plant that is 17 cm tall grows 2 cm each week.

a) Continue the sequence

17, ___, _____, _____

1 week, 2 weeks, 3 weeks

b) How tall will the plant be after three weeks ?

c) After how many weeks will the plant be 27 cm tall?

Solution :

a)  Every week it grows 2 cm.

17, (17 + 2), (19 + 2), (21 + 2)

Week 1 = 19

Week 2 = 21

Week 3 = 23

b) After 3 weeks,

the height of the plant is 23 cm

c)  When height = 27

t_n = a + (n - 1) d

a = 17 and d = 2

t_n = 17 + (n - 1) (2)

27 = 17 + (n - 1) (2)

27 - 17 = 2(n - 1)

10 = 2(n - 1)

10/2 = n - 1

5 = n - 1

n = 5 + 1

n = 6

So, after 6 weeks the height of the plant is 27 cm.

Example 11 :

Make a pattern to solve the problem.

a) Hanna has $49. She spends $8 each day. How much money does she have left after 5 days ?

b) Matt has roll of 74 stamps. He uses 7 stamps each day for 4 days. How many stamps are left ?

Solution :

a) To find the amount left after 5 days, we have to find the first 5 terms.

49, (49-8), (41 - 8), (33 - 8), (25 - 8),. .....

49, 41, 33, 25, 17,............

So after 5 days $17 is the left.

b) Number of stamps initially = 74

To find the number of stamps after 4 days, we have to find the 4th term.

Number of stamps uses = 4

tn = a + (n - 1) d

= 74 + (4 - 1)(4)

= 74 + 3(4)

= 74 + 12

= 86

So, number of stamps after 4 days is 86.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.