FIND THE SLOPE OF A LINEAR FUNCTION

Slope of a linear function is the change in y for a unit change in x along the line and usually denoted by the letter "m"

Slope is sometimes referred to as "rise over run".

Because the fraction consists of the rise (the change in y, going up or down) divided by the run (the change in x, going from left to the right).

The figure shown below illustrated this. 

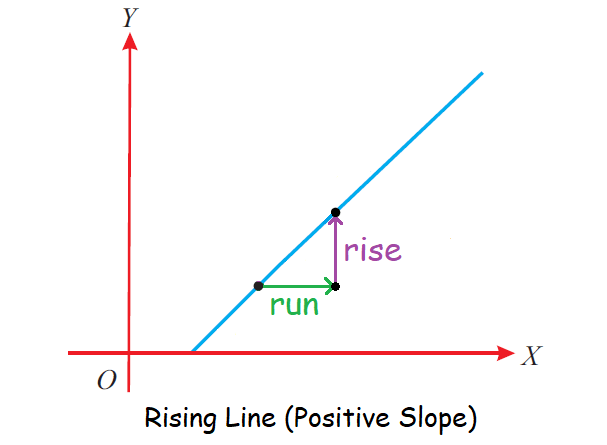
Finding Slope Using the Two Points on the Line

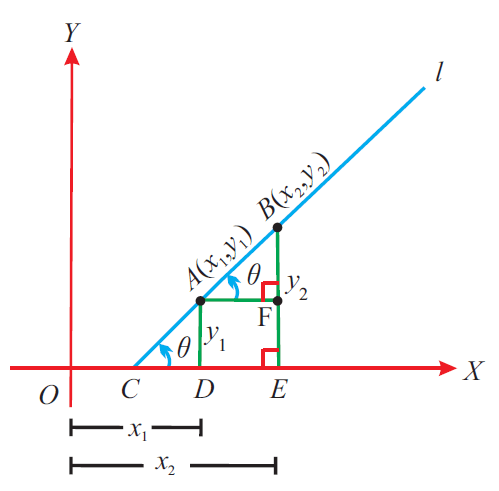
From the above figure, the slope of the straight line joining the points A (x₁, y₁) and B (x₂, y₂) is   

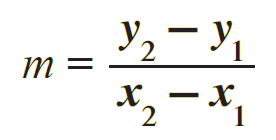
Examples

Example 1 :

Find the slope of the line shown below.

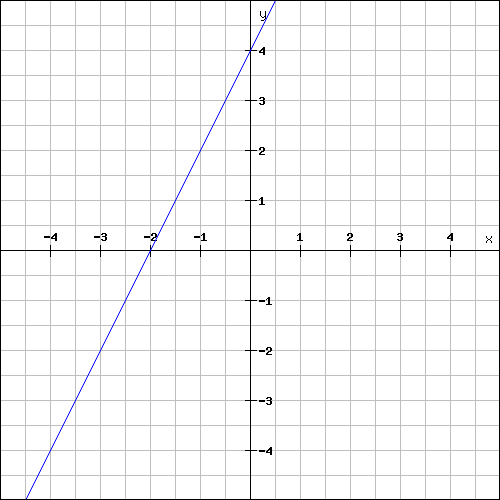
Solution :

The above line is a rising line.

So, its slope will be a positive value.

Plot the two points (-2, 0) and (0, 4) on the line and measure the rise and run. 

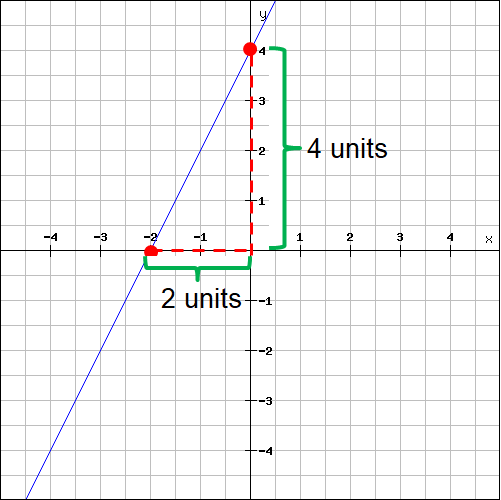
For the above line, 

Rise  =  4

Run  =  2

Then, slope is 

m  =  rise / run

m  =  4/2

m  =  2

Alternative Method : 

Formula to find slope is

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁)  =  (-2, 0) and (x₂, y₂)  =  (0, 4) 

m  =  (4 - 0) / (0 + 2)

m  =  4/2

m  =  2

Example 2 :

Find the slope of the line shown below.

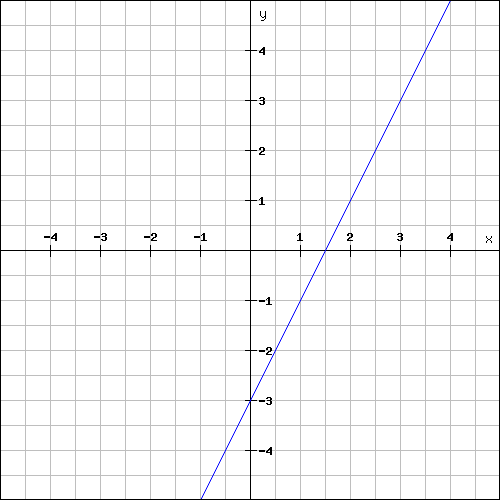
Solution :

The above line is a rising line line.

So, its slope will be a positive value.

Plot the two points (1, -1) and (2, 1) on the line and measure the rise and run. 

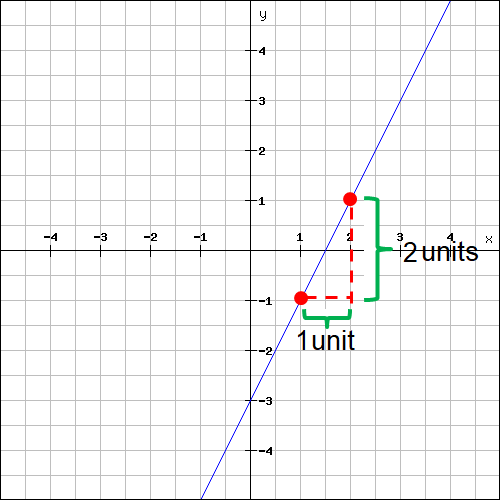
For the above line, 

Rise  =  2

Run  =  1

Then, slope is 

m  =  rise / run

m  =  2/1

m  =  2

Alternative Method : 

Formula to find slope is

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁)  =  (1, -1) and (x₂, y₂)  =  (2, 1) 

m  =  (1 + 1) / (2 - 1)

m  =  2/1

m  =  2

Example 3 :

Find the slope of the line shown below.

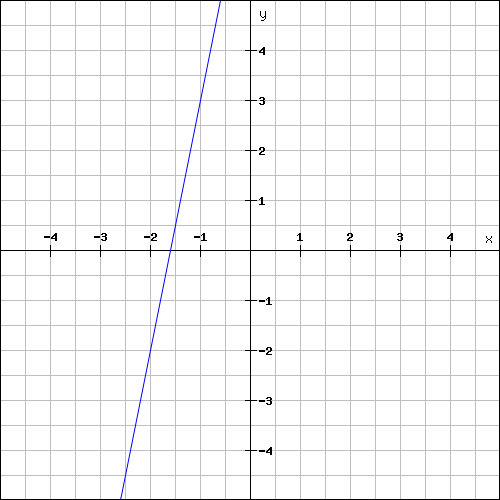
Solution :

The above line is a rising line line.

So, its slope will be a positive value.

Plot the two points (-2, -2) and (-1, 3) on the line and measure the rise and run. 

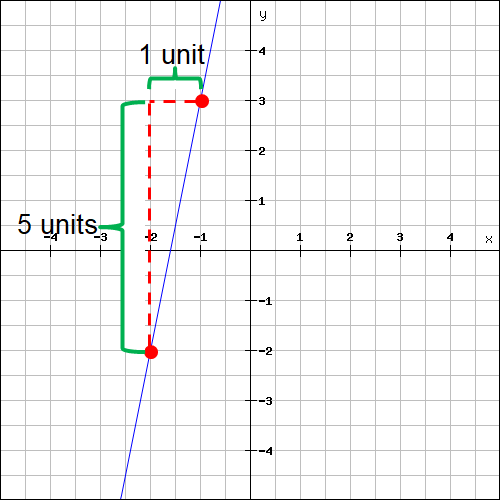
For the above line, 

Rise  =  5

Run  =  2

Then, slope is 

m  =  rise / run

m  =  5/1

m  =  5

Alternative Method : 

Formula to find slope is

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁)  =  (-2, -2) and (x₂, y₂)  =  (-1, 3) 

m  =  (3 + 2) / (-1 + 2)

m  =  5/1

m  =  5

Example 4 :

Find the slope of the line shown below.

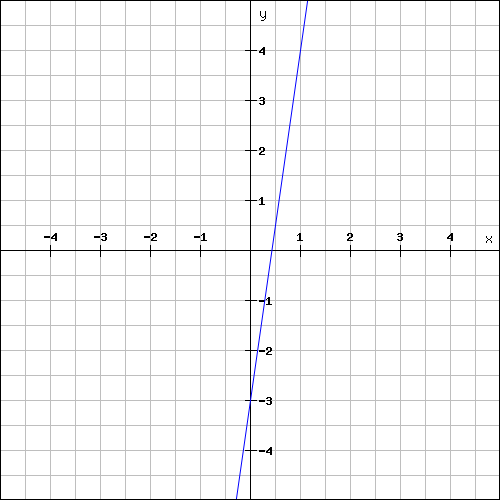
Solution :

The above line is a rising line line.

So, its slope will be a positive value.

Plot the two points (0, -3) and (1, 4) on the line and measure the rise and run. 

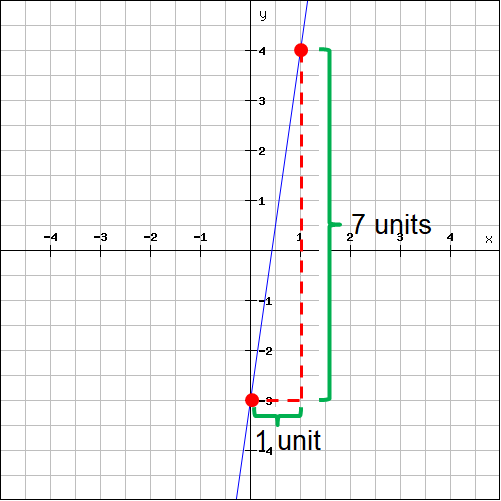
For the above line, 

Rise  =  7

Run  =  1

Then, slope is 

m  =  rise / run

m  =  7/1

m  =  7

Alternative Method : 

Formula to find slope is

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁)  =  (0, -3) and (x₂, y₂)  =  (1, 4) 

m  =  (4 + 3) / (1 - 0)

m  =  7/0

m  =  7

Example 5 :

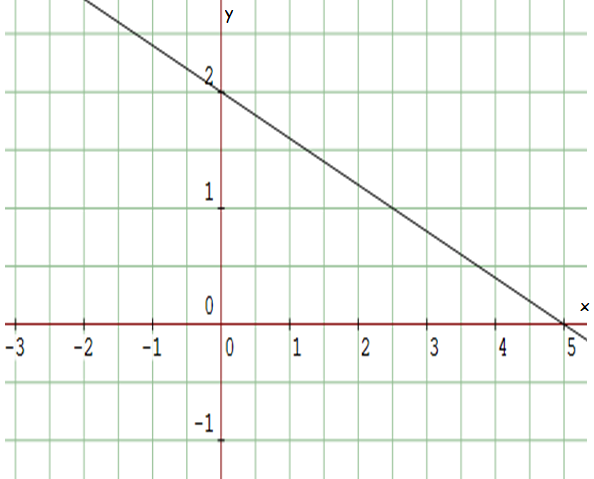
Solution :

The above line is a rising line line.

So, its slope will be a positive value.

Plot the two points (0, 2) and (5, 0) on the line and measure the rise and run. 

Since it is falling line, it will have negative slope.

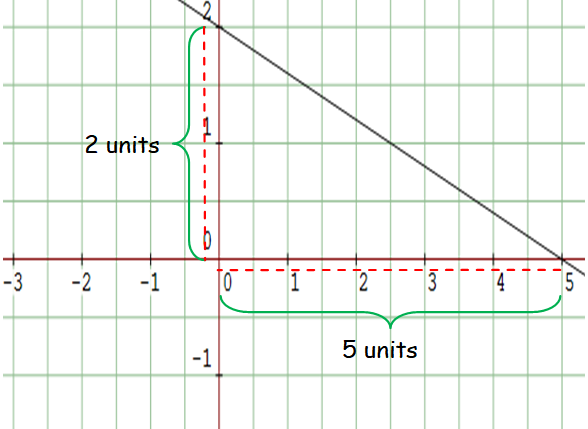
For the above line, 

Rise  =  2

Run  =  5

Then, slope is 

m  =  rise / run

m  =  -2/5

Alternative Method : 

Formula to find slope is

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁)  =  (0, 2) and (x₂, y₂)  =  (5, 0) 

m  =  (0 - 2) / (5 - 0)

m  =  -2/5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.