FIND THE SUM OF ALL MULTIPLES BETWEEN TWO NUMBERS

Question 1 :

How many three digit numbers are divisible by 7?

Solution :

The first three digit number is 100 and the last three digit number is 999

Now we should find the number of three digit terms which are divisible by 7.

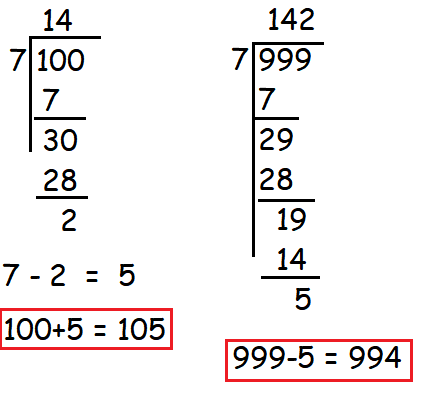
105 is the first three digit number divisible by 7 and 994 is the last three digit number which is divisible by 7.

 105 + 112 + ........... + 994

a_n = a + (n - 1) d

a = 105, d = 112 - 105  = 7 

994  =  105 + (n - 1)7

994 - 105  =  (n - 1)7

889  =  (n- 1)7

889/7  =  n - 1

127  =  n - 1

n  =  127 + 1

n  =  128

Hence there are 128 three digit numbers are divisible by 7.

Question 2 :

How many multiples of 4 lie between 10 and 250? 

Solution :

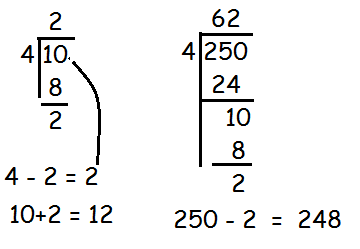
12, 16, 20,.......................,248

 a_n = a + (n - 1) d

a = 12      d = 16 - 12 = 4       a_n = 248   

248  =  12 + (n - 1) 4

248 - 12  =  (n - 1) 4

236  =  (n - 1) 4

236/4  =  n - 1

59  =  n - 1

n  =  59 + 1

n  =  60

Question 3 :

For what value of n, are the nth terms of two APs 63, 65, 67,....... and 3, 10, 17,........ equal?

Solution :

Let a_n and b n are two n^th terms of the given sequence respectively.

(1)  =  (2)

a_n = b_n

63 + (n - 1) 2  =  3 + (n - 1) 7

63 + 2 n - 2  =  3 + 7n - 7

61 + 4  =  7 n - 2 n

65  =  5 n

n  =  65/5

n  =  13  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.