FIND THE VALUE OF B THAT MAKES THE FUNCTION CONTINUOUS

Question 1 :

Find the constant b that makes g continuous on (−∞, ∞)

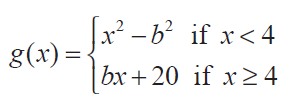
Solution :

Since the function is continuous at the point x = 4, then

lim _{x-> 4-} f(x)  =  lim _{x-> 4+} f(x)

lim _{x-> 4-} f(x)  =  lim _{x-> 4-} x² - b²

=  4² - b²

=  16 - b²   ----(1)

lim _{x-> 4+} f(x)  =  lim _{x-> 4+-} bx + 20 

=  b(4) + 20

=  4b + 20  ----(2)

(1)  =  (2)

16 - b²  =  4b + 20

b² + 4b + 20 - 16  =  0

b² + 4b + 4 =  0

(b + 2)(b + 2)  =  0

b + 2   =  0

b  =  -2

Hence the value of b is -2.

Question 2 :

Consider the function f (x) = x sin π/x What value must we give f(0) in order to make the function continuous everywhere?

Solution :

f (x) = x sin π/x 

Range of sin x is [-1, 1]

-1  ≤ sin π/x  ≤ 1

By multiplying x throught the equation, we get

-x  ≤ x (sin π/x)  ≤ x

Now let us apply the limit values

lim _{x -> 0} (-x)  ≤ lim _{x -> 0} x (sin π/x)  ≤ lim _{x -> 0} x

0 ≤ lim _{x -> 0} x (sin π/x)  ≤ 0

By sandwich theorem 

lim _{x -> 0} x (sin π/x)  =  0

Now let us redefine the function

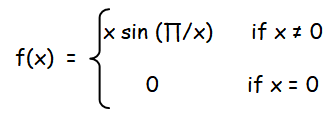
From this we come to know the value of f(0) must be 0,  in order to make the function continuous everywhere

Question 3 :

The function f(x)  =  (x² - 1) / (x³ - 1) is not defined at x = 1. What value must we give f(1) inorder to make f(x) continuous at x = 1 ?

Solution :

By applying the limit value directly in the function, we get 0/0.

Now let us simplify f(x)

f(x)  =  (x² - 1) / (x³ - 1)

  =  (x + 1) (x - 1)/(x - 1)(x² + x + 1)

  =  (x + 1) / (x² + x + 1)

lim _{x-> 1} f(x)   = lim _{x-> 1}  (x + 1) / (x² + x + 1)

  =  (1 + 1)/ (1 + 1 + 1)

  =  2/3

By redefining the function, we get

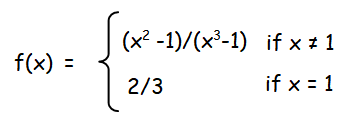
From this we come to know the value of f(1) must be 2/3,  in order to make the function continuous everywhere

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.