FIND TRANSLATION OF A POINT ALONG THE GIVEN VECTOR

A translation moves an object from one place to another. Every point on the object moves the same distance in the same direction.

If P(x, y) is translated

h units in the x-direction and

k units in the y-direction

to become P'(x', y'), then

x' = x + h and y' = y + k

x'  =  x + h and y'  =  y + k are called transformation equations.

Example 1 :

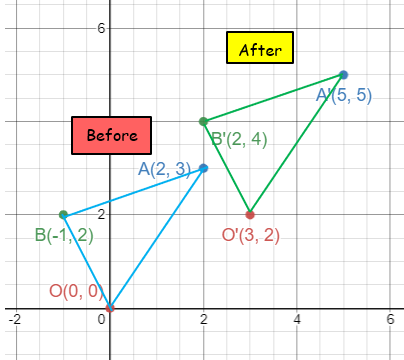
Triangle OAB with vertices O(0, 0), A(2, 3) and B(-1, 2) is translated under the vector <3, 2>. Find the image vertices and illustrate the object and the image.

Solution :

To find vertices of image after translation, we use 

x'  =  x+h and y'  =  y+k

Here (h, k)  ==>  (3, 2)

x'  =  x+3 and y'  =  y+2

Example 2 :

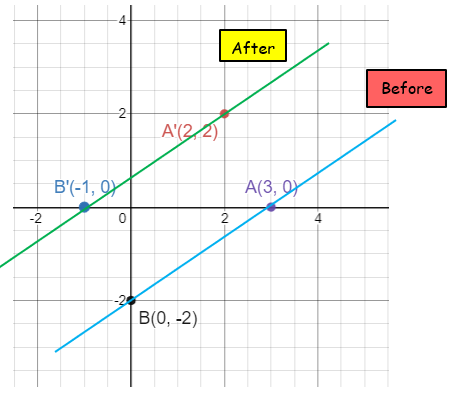
Find the image equation when 2x-3y  =  6 is translated under the vector <-1, 2>.

Solution :

Let us find any two point on the straight line 2x-3y  =  6.

Converting 2x-3y  =  6 into intercept form, we get

(2x/6)-(3y/6)  =  6/6

x/3 - y/2  =  1

Point on x-intercept is (3, 0).

Point on y-intercept is (0, -2).

Here (h, k)  ==>  (-1, 2)

x'  =  x-1 and y'  =  y+2

Example 3 :

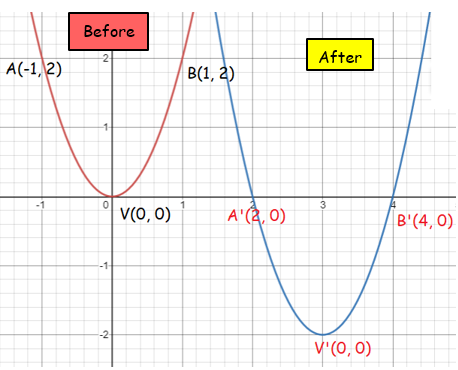
Find the image of y = 2x² under a translation with vector <3, -2>.

Solution :

Let us find any three points on the parabola.

Vertex of the parabola is (0, 0)

If x  =  -1, then y  =  2

If x  =  1, then y  =  2

So three point on the parabola are V(0, 0), A(-1, 2) and B(1, 2)

The image has to be translated along the vector <3, -2>.

(h, k) ==>  (3,-2)

x'  =  x+3 and y'  =  y-2

To find equation of new cure, let us find value of x and y from x'  =  x+3 and y'  =  y-2

x  =  x'-3 and y  =  y+2

Given curve :

y  =  2x²

Equation of curve after translation :

y+2  =  2(x-3)²

y+2  =  2(x²-6x+9)

y+2  =  2x²-12x+18

y  =  2x²-12x+16

Example 4 :

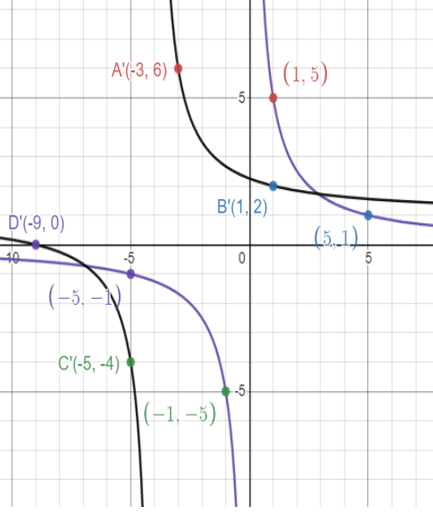
Find the image of xy  =  5 under a translation with vector <-4, 1>.

Solution :

xy  =  5

Finding 4 point on the rectangular hyperbola,

y  =  5/x

If x  =  1, then y  =  5  ==> A(1, 5)

If x  =  5, then y  =  1  ==> B(5, 1)

If x  =  -1, then y  =  -5  ==> C(-1, -5)

If x  =  -5, then y  =  -1  ==> D(-5, -1)

Here (h, k)  ==>  (-4, 1)

x'  =  x-4 and y'  =  y+1

Equation of curve before translation :

xy  =  5

Equation of curve after translation :

x'  =  x-4 and y'  =  y+1

x  =  x'+4 and y  =  y'-1

By applying x as x'+4 and y as y-1, we get

(x+4)(y-1)  =  5

xy-4x+4y-4-5  =  0

xy-4x+4y-9  =  0

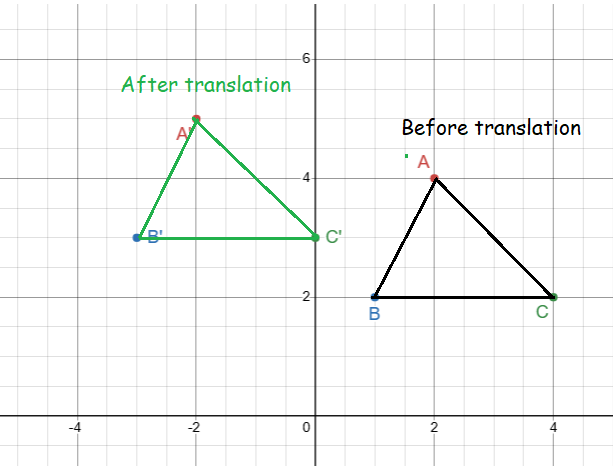
Draw the preimage and image of each triangle under a translation along (-4, 1).

Example 5 :

Triangle with coordinates 

A (2, 4) B (1, 2) and C (4, 2).

Solution : 

Translation vector is (-4, 1), then move each 4 units left and 1 unit up. Original points will be in the form (x, y), after translation the new points will be in the form (x - 4, y + 1)

• A(2, 4) ==> A'(2 - 4, 4 + 1) ==> A'(-2, 5)
• B(1, 2) ==> B'(1 - 4, 2 + 1) ==> B'(-3, 3)
• C(4, 2) ==> C'(4 - 4, 2 + 1) ==> C'(0, 3)

Example 6 :

A translation along the vector 〈−2, 7〉 maps point P to point Q. The coordinates of point Q are (4, −1) . What are the coordinates of point P? Explain your reasoning.

Solution : 

Translation vector is (-2, 7). Point P is translation with the translation vector and get the new position Q(4, -1).

(x, y) ==> (x + h, y + k)

Here (x - 2, y + 7)

P(x - 2, y + 7) ==> Q(4, -1)

x - 2 = 4 and y + 7 = -1

x = 4 + 2, y = -1 - 7

x = 6, y = -8

So, the required point is P(6, -8)

Example 7 :

Find the coordinates of the image under the transformation ⟨6, -11⟩.

a)  (x, y) ==>         b) (2, -3) ==>

c)  (3, 1) ==>         d)  (4, -3) ==>

Solution :

The given transformation is (6, -11).

• a)  (x, y) ==>  (x + 6, y - 11)
• b) (2, -3) ==> (2 + 6, -3 - 11) ==> (8, -14)
• c)  (3, 1) ==> (3 + 6, 1 - 11) ==> (9, -10)
• d)  (4, -3) ==> (4 + 6, -3 + 11) ==> (10, 8)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.