FIND VALUES OF INVERSE FUNCTIONS FROM TABLES

Example 1 :

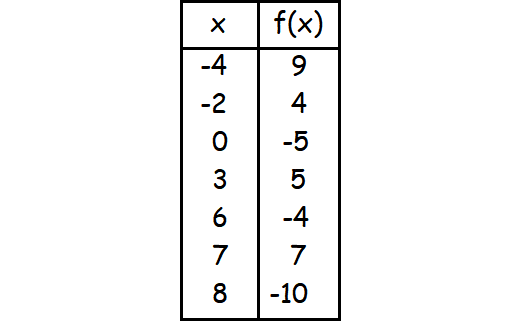
Use the table below to find the following if possible : 

(i)  f ^-1(- 4) 

(ii)  f ^-1(6)

(iii)  f ^-1(9)

(iv)  f ^-1(10)

(v)  f ^-1(-10)

Solution :

(i) f^-1(-4)

a = f^-1(- 4) if and only if f(a) = -4

In the above table, f(x) = -4 for x = 6.

f(6) = -4

f^-1(-4) = 6

(ii) f^-1(6)

a = f^-1(6) if and only if 6 = f(a)

We don't find the value 6 in the column f(x).

Hence f ^-1(6) is undefined.

(iii) f^-1(9)

c = f^-1(9) if and only if f(c) = 9

In the above table, f(x) = 9 for x = -4.

f(-4) = 9

f^-1(9) = -4

(iv) f^-1(10)

d = f^-1(10) if and only if f(d) = 10.

We don't find the value 10 in the column f(x).

Hence f^-1(10) is undefined.-

(v) f^-1(-10)

e = f^-1(-10) if and only if f(e) = -10.

In the above table, f(x) = -10 for x = 8.

f(8) = -10

f^-1(-10) = 8

Determine whether each pair of functions f and g are inverses. Explain your reasoning.

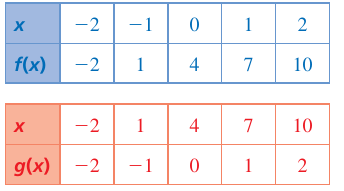
Example 2 :

Solution :

Ordered pairs of the function f(x) :

(-2, -2) (-1, 1) (0, 4) (1, 7) (2, 10)

Ordered pairs of the function g(x) :

(-2, -2) (1, -1) (4, 0) (7, 1) (10, 2)

Domain of f(x) = Range of g(x)

Range of f(x) = Domain of g(x)

So, the functions are inverse to each other.

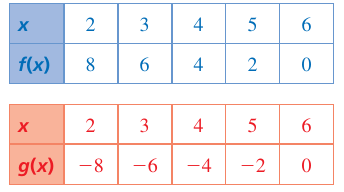
Example 3 :

Solution :

Ordered pairs of the function f(x) :

(2, 8) (3, 6) (4, 4) (5, 2) (6, 0)

Ordered pairs of the function g(x) :

(2, -8) (3, -6) (4, -4) (5, -2) (6, 0)

Domain of f(x) ≠ Range of g(x)

Range of f(x) ≠ Domain of g(x)

So, the functions are not inverse to each other.

Example 4 :

What is the inverse of the function whose graph is shown?

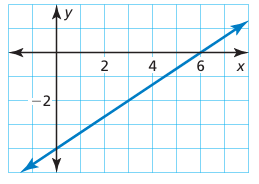
a) g(x) = (3/2)x - 6       b)  g(x) = (3/2)x + 6

c)  g(x) = (2/3)x - 6      d)  g(x) = (2/3)x + 12

Solution :

Equation of the line shown :

y-intercept = -4

Points on the line (3, -2) and (6, 0)

Slope = (y₂ - y₁)/(x₂ - x₁)

= (0 - (-2))/(6 - 3)

= (0 + 2) / 3

= 2/3

y - y₁ = m(x - x₁)

y - (-2) = (2/3) (x - 3)

y + 2 = (2/3) (x - 3)

y = (2/3)x - (2/3) 3 - 2

y = (2/3)x - 2 - 2

y = (2/3)x - 4

To find the inverse function, 

Put y = x and x = y

x = (2/3)y - 4

Solving for y :

x + 4 = (2/3)y

y = (3/2)(x + 4)

y = (3/2) x + (3/2)(4)

y = (3/2) x + (3)2

y = (3/2) x + 6

Change y = g(x)

g(x) = (3/2) x + 6

So, option b is correct.

Example 5 :

f(x) = x/(x + 3)

a) if f^-1(x) = -5, find the value of x.

b) Show that ff^-1 (x) = x

Solution :

f(x) = x/(x + 3)

a)

Finding inverse :

y = x/(x + 3)

Put x = y and y = x

x = y/(y + 3)

x(y + 3) = y

xy + 3x = y

3x = y - xy

3x = y(1 - x)

3x/(1 - x) = y

f^-1(x) = 3x/(1 - x)

When  f^-1(x) = -5

5 = 3x/(1 - x)

5(1 - x) = 3x

5 - 5x = 3x

5 = 3x + 5x 

8x = 5

x = 5/8

b)  ff^-1 (x) = x

Applying x = 3x/(1 - x) in the function f(x) as x.

f(3x/(1 - x)) = [3x/(1 - x)]/[3x/(1 - x)) + 3]

= [3x/(1 - x)]/[3x + 3(1 - x)/(1 - x)]

= [3x/(1 - x)]/[(3x + 3 - 3x)/(1 - x)]

= [3x/(1 - x)]/[3/(1 - x)]

= [3x/(1 - x)] ⋅ [(1 - x)/3]

= x

Example 6 :

𝑓(𝑥) = 2𝑥 + 𝑐 𝑔(𝑥) = 𝑐𝑥 + 5 𝑓𝑔(𝑥) = 6𝑥 + 𝑑

𝑐 and 𝑑 are constants. Work out the value of 𝑑.

Solution :

𝑓(𝑥) = 2𝑥 + 𝑐

𝑔(𝑥) = 𝑐𝑥 + 5

𝑓𝑔(𝑥) = 6𝑥 + 𝑑

f(cx + 5) = 6x + d

2(cx + 5) = 6x + d

2cx + 10 = 6x + d

2c = 6 and d = 10

c = 3 and d = 10

Answer the following. Assume that f and g are defined for all real numbers. 

Example 7 :

If f and g are inverse functions f(-2) = 3 and f(4) = -2, find g(-2)

Solution :

When f and g are inverse to each other 

(-2, 3) (4, -2) are the ordered pairs of the function f, then (3, -2) and (-2, 4) are the ordered pairs of the function g.

So, the value of g(-2) is 4.

Example 8 :

If f and g are inverse functions, f(7) = 10 and f(10) = -1 find g(10)

Solution :

Ordered pairs of f are (7, 10) and (10, -1)

Ordered pairs of g are (10, 7) and (-1, 10)

Then the value of g(10) is 7.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.