FINDING ANGLES INVOLVING ISOCELES TRIANGLE

Problem 1 :

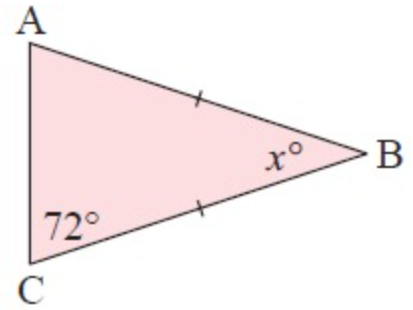
Solution :

Given,  AB  =  BC and <ABC  =  xº

<BAC  =  <BCA  =  72º

In triangle ABC.

<BAC + <BCA + <ABC  =  180º

72º + 72º + xº =  180º

144º+ xº  =  180º

    xº =  180º - 144º

xº  =  36º

Problem 2 :

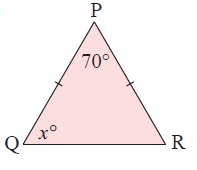
Solution :

Given,  PQ  =  QR and <PQR  = xº

<QPR  =  70º and  <PRQ  =  xº

In triangle PQR.

<QPR + <PRQ + <PQR =  180º

70º + xº + xº =  180º

70º + 2xº = 180º

2xº = 180º - 70º

2xº =  110º

xº =  110/2

xº =  55º

Problem 3 :

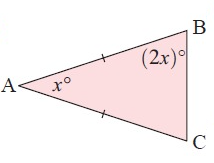
Solution :

Given,  AB  = AC and <BAC  = xº

<ABC   =  <BCA  =  (2x)º

In triangle ABC.

<ABC + <BCA + <BAC =  180º

(2x)º + (2x)º + xº = 180º

4xº + xº = 180º

5xº =  180º

xº =  180º/5

xº = 36º

Problem 4 :

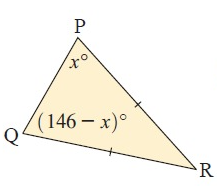
Solution :

Given,  PR  = QR and <QPR  =  xº

Since PR and QR are equal, it is isosceles triangle.

<PQR  =  <QRP  = (146-x)º

x  =  146-x

x+x  =  146

2x  =  146

x  =  73

So, the value of x is 73.

Problem 5 :

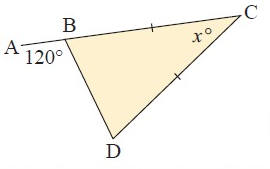
Solution :

Given, BC  =  BD and <BCD  =  xº

<CBD  =  <BDC  =  60º

In triangle ABCD,

<DBC + <ADB + <BCD = 180º

60º + 60º + xº = 180º

xº  =  180º - 120

xº  =  60º

Problem 6 :

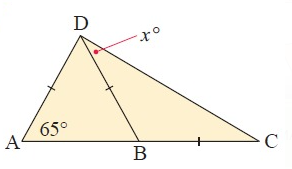
Solution :

Given, AD  =  BD  =  BC and <BDC  =  xº

<DBA =  <BAD  =  65º

<ABD + <DBC  =  180

65 + <DBC  =  180

<DBC  =  180-65

<DBC  =115

<BDC  =  <BCD  =  x

In triangle BDC.

<BDC + <DBC + <DCB  =  180

x+115+x  =  180

2x+115  =  180

2x  =  65

x  =  65/2

Problem 7 :

In the figure given below, PQ = PS. The value of x is 

a)  35    b)  45     c)  55     d) 70

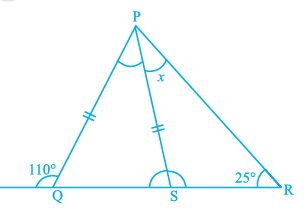
Solution :

<PQS = 180 - 110 ==> 70

Since PQ and PS are equal, <PQS = <PSQ

<PSQ = 70

In triangle PQS,

<PQS + <PSQ + <SPQ = 180

70 + 70 + <SPQ = 180

<SPQ = 180 - 140

<SPQ = 40

In triangle PQR,

<PQR + <QPR + <PRQ = 180

70 + <QPS + <SPQ + 25 = 180

95 + 40 + <SPQ = 180

135 + <SPQ = 180

<SPQ = 180 - 135

<SPQ = 45

So, option b is correct.

Problem 8 :

Find the measures of the angles of an isosceles triangle if the measure of the vertex angle is 40 degrees less than the sum of the measures of the base angles.

Solution :

Let x be the base angles.

Vertex angle = (x + x) - 40

= 2x - 40

Sum of interior angles of a triangle = 180

x + x + 2x - 40 = 180

4x - 40 = 180

4x = 180 + 40

4x = 220

x = 220/4

x = 55

Applying x = 45 in 2x - 40

= 2(55) - 40

= 110 - 40

= 70

So, the required angles are 55, 55 and 70.

Problem 9 :

In an isosceles triangle, one angle is 70°. The other two angles are of

(i) 55° and 55° (ii) 70° and 40° (iii) any measure

In the given option(s) which of the above statement(s) are true?

(a) (i) only      (b) (ii) only    (c) (iii) only     (d)  (i) and (ii)

Solution :

In any isosceles triangle, two angle measures will be equal. We are not sure about the given angle is equal angles or not. 

Case 1 :

Let the given angle be equal angle measures of isosceles triangle.

Let the other angle be x

70 + 70 + x = 180

x = 180 - 140

x = 40

In this case, the required angles are 40, 70 and 70

Case 2 :

Let the given angle measure be vertex angle, then the two base angles are being considered as x.

x + x + 70 = 180

2x + 70 = 180

2x = 180 - 70

2x = 110

x = 110/2

x = 55

In this case, the required angles are 55, 55 and 70.

So, option d is correct.

Problem 10 :

In a triangle, one angle is of 90°. Then

(i) The other two angles are of 45° each

(ii) In remaining two angles, one angle is 90° and other is 45°

(iii) Remaining two angles are complementary In the given option(s) which is true?

(a) (i) only      (b) (ii) only      (c) (iii) only     (d) (i) and (ii)

Solution :

In a triangle, sum of interior angles will be equal to 180.

Since one angle measure is 90, then the sum of the other two angles measures should be 90. Which means they should be complementary angles. So, option c is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.