FINDING AREA OF QUADRILATERAL PARALLELOGRAM AND RHOMBUS WORD PROBLEMS

Problem 1 :

Find the area of the unshaded region.

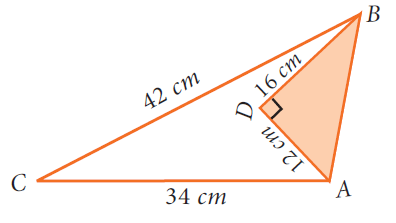
Solution :

<BDA  =  90

AB²  =  DA² + DB²

AB²  =  12² + 16²

AB²  =  144 + 256

AB²  =  400

AB  =  20

Area of unshaded region  =  Area of ACB - Area of ADB

Area of ACB :

AC  =  34 cm, BC  =  42 cm and AB  =  20

s  =  (a + b + c)/2

s  =  (34 + 42 + 20)/2

s  =  48

s - a  =  48 - 34  =  14, s - b  =  48 - 42  =  6

and s - c  =  48 - 20  =  28

  =  √s(s - a) (s - b) (s - c)

  =  √48 ⋅ 14 ⋅ 6 ⋅ 28

  =  336 cm²

 Area of ADB :

DB  =  16 cm, DA  =  12 cm and AB  =  20

s  =  (16 + 12 + 20)/2

  s  =  48/2  =  24

s - a  =  24 - 16  =  8, s - b  =  24 - 12  =  12

and s - c  =  24 - 20  =  4

  =  √24 ⋅ 8 ⋅ 12 ⋅ 4

  =  96 cm²

Area of unshaded region  =  336 - 96

  =  240 cm²

Problem 2 :

Find the area of a quadrilateral ABCD whose sides are AB = 13cm, BC = 12cm, CD = 9cm, AD = 14cm and diagonal BD = 15cm.

Solution :

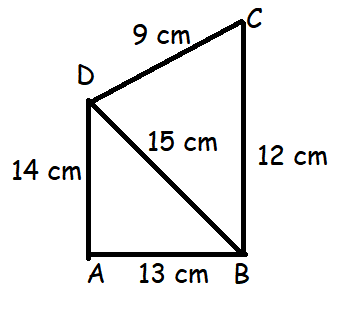
Area of quadrilateral ABCD  =  Area of ADB+Area of DBC

Area of ADB :

a = 13, b = 15, c = 14

s  =  (13 + 15 + 14)/2  =  21

  =  √21(21 - 13) (21 - 15) (21 - 14)

  =  √21 ⋅ 8 ⋅ 6 ⋅ 7

  =  84 cm²

Area of BDC :

a = 12, b = 9, c = 15

s  =  (12 + 9 + 15)/2  =  18

  =  √18(18 - 12) (18 - 9) (18 - 15)

  =  √18 ⋅ 6 ⋅ 9 ⋅ 3

  =  54 cm²

Area of quadrilateral  =  84 + 54

  = 138 cm²

Problem 3 :

A park is in the shape of a quadrilateral. The sides of the park are 15 m, 20 m, 26 m and 17 m and the angle between the first two sides is a right angle. Find the area of the park.

Solution :

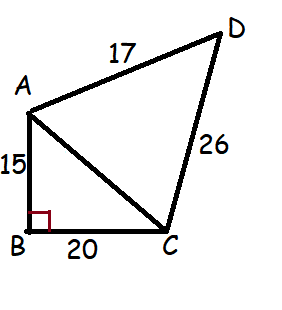
In triangle ABC,

AC²  =  AB² + BC²

AC²  =  15² + 20²

AC²  =  225 + 400

AC  =  √625  =  25

Area of quadrilateral ABCD  =  Area of ABC+Area of ADC

Area of ABC :

a = 15, b = 20, c = 25

s  =  (15 + 20 + 25)/2  =  30

  =  √30(30 - 15) (30 - 20) (30 - 25)

  =  √30 ⋅ 15 ⋅ 10 ⋅ 5

  =  150 cm²

Area of ADC :

a = 17, b = 26, c = 25

s  =  (17 + 26 + 25)/2  =  34

  =  √34(34 - 17) (34 - 26) (34 - 25)

  =  √34 ⋅ 17 ⋅ 8 ⋅ 9

  =  204 cm²

Area of quadrilateral  =  150 + 204

=  354 cm²

Problem 4 :

The front of an A-frame house is in the shape of a triangle. The height of the house is 20 feet. The area of the front of the A-frame is 600 square feet. Write and solve an equation to find the base of the A-frame house.

Solution :

Area of the frame in the shape of triangle

= 600 square feet

(1/2) x base x height = 600

height = 20 ft

(1/2) x base x 20 = 600

base x 10 = 600

base = 600/10

base = 10 ft

So, the required base of the triangle is 10 ft.

Problem 5 :

One side of a parallelogram is 18 cm and its distance from the opposite side is 8 cm. The area of the parallelogram

Solution :

Base = 18 cm

Height = 8 cm

Area of parallelogram = base x height

= 18 x 8

= 144 cm²

Problem 6 :

A parallelogram has sides 30 m and 14 m and one of its diagonals is 40 m long. then the area is :

Solution :

In parallelogram, opposite sides will be equal. The triangle created by the sides of the parallelogram and diagonal.

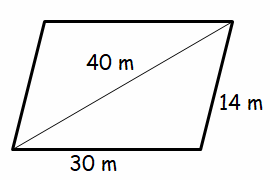
a = 30, b = 14, c = 40

s  =  (30 + 14 + 40)/2  =  42

Area of isosceles triangle

= √42(42 - 30) (42 - 14) (42 - 40)

  =  √42 ⋅ 12 ⋅ 28 ⋅ 2

= 168

Area of parallelogram = 168 (2)

= 336 m²

Problem 7 :

A triangle and parallelogram are constructed on the same base such that their areas are equal. If the altitude of the parallelogram is 100 m, then the altitude of the triangle is 

a)  10√2 m     b)  100 m     c)  100√2 m      d)  200 m

Solution :

When triangle and parallelogram are at the same base their areas will be equal.

base x height = (1/2) x base x height

Altitude of parallelogram = 100 m

base x 100 = (1/2) x base x height

Since the two shapes are having same base,

100 = (1/2) x h

h = 100(2)

= 200 m

So, the required height of the triangle is 200 m. Option d is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.