FINDING CONTINUITY OF PIECEWISE FUNCTIONS

Question 1 :

A function f is defined as follows :

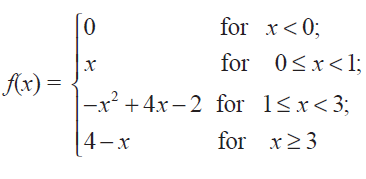
Is the function continuous?

Solution :

(i) First let us check whether the piece wise function is continuous at x = 0.

For the values of x lesser than 0, we have to select the function f(x)  =  0.

lim _x->0- f(x)  =  lim _x->0- 0

  =  0 -------(1)

For the values of x greater than 0, we have to select the function f(x)  =  x.

lim _x->0+ f(x)  =  lim _x->0+ x

  =  0  -------(2)

lim _x->0- f(x) = lim _x->0+ f(x)

Hence the function is continuous at x = 0.

(ii) Let us check whether the piece wise function is continuous at x = 1.

For the values of x lesser than 1, we have to select the function f(x)  =  x.

lim _x->1- f(x)  =  lim _x->1- 0

  =  1 -------(1)

For the values of x greater than 1, we have to select the function f(x)  =  -x² + 4x - 2.

lim _x->1+ f(x)  =  lim _x->1+ (-x² + 4x - 2)

  =  -1² + 4(1) - 2

=  -1 + 4 - 2

=  1  -------(2)

lim _x->1- f(x) = lim _x->1+ f(x)

Hence the function is continuous at x = 1.

(iii) Let us check whether the piece wise function is continuous at x = 3.

For the values of x lesser than 3, we have to select the function f(x)  =  -x² + 4x - 2.

lim _x->3- f(x)  =  lim _x->3- -x² + 4x - 2

  =  -3² + 4(3) - 2

=  -9 + 12 - 2

=  -11 + 12

  =  1  -------(1)

For the values of x greater than 3, we have to select the function f(x)  =  4 - x

lim _x->3+ f(x)  =  lim _x->3+ 4 - x

=  4 - 3

=  1  -------(2)

lim _x->3- f(x) = lim _x->3+ f(x)

Hence the function is continuous at x = 3.

Question 2 :

Find the points of discontinuity of the function f, where

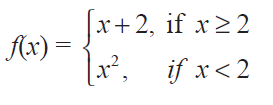
Solution :

For the values of x greater than 2, we have to select the function x + 2.

lim _x->2- f(x)  =  lim _x->2- x + 2

  =  2 + 2

       =  4  -------(1)

For the values of x lesser than 2, we have to select the function x².

lim _x->2+ f(x)  =  lim _x->2+ x²

  =  2²

       =  4-------(2)

lim _x->2- f(x) =  lim _x->2+ f(x)

The function is continuous at x = 2.

Hence the given piecewise function is continuous for all x ∈ R.

Question 3 :

Find the points of discontinuity of the function f, where

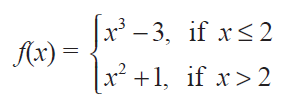
Solution :

For the values of x greater than 2, we have to select the function x² + 1

lim _x->2- f(x)  =  lim _x->2- x² + 1

  =   2² + 1

       =  5  -------(1)

For the values of x lesser than 2, we have to select the function x³ - 3.

lim _x->2+ f(x)  =  lim _x->2+ x³ - 3

  =  2³ - 3

=  8 - 3

       =  5-------(2)

lim _x->2- f(x) =  lim _x->2+ f(x)

The function is continuous at x = 2.

Hence the given piecewise function is continuous for all x ∈ R.

Question 4 :

Find the points of discontinuity of the function f, where

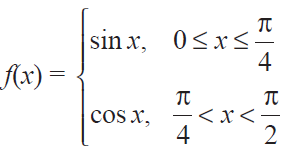
Solution :

Here we are going to check the continuity between 0 and π/2.

For the values of x lesser than or equal to π/4, we have to choose the function sin x.

lim _x->π/4- f(x)  =  lim _x->π/4^- sin x

       =  sin (π/4)

=  1/√2

For the values of x greater than π/4, we have to choose the function cos x .

lim _x->π/4+ f(x)  =  lim _x->π/4⁺ cos x

       =  cos (π/4)

=  1/√2

The function is continuous for all x ∈ [0, π/2).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.