FINDING DOMAIN FOR RATIONAL FUNCTIONS

The domain of a rational function includes all real numbers except those that cause the denominator equal to zero.

Question 1 :

Find the domain of each of the following real values functions.

f(x)  =  (x - 1)/(x - 3)

Solution :

Domain means set of all possible values of x. To get the values for which the function be undefined, we have to equate the denominator to 0.

x - 3  =  0

x  =  3

Clearly, for the value x = 3 the function will become undefined. So, the domain is set of all real numbers except 3. 

Hence R - {3} is the domain of the given function.

(ii)  f(x)  =  (2x - 3)/(x² - 3x + 2)

Solution :

In order to find domain, let us equate the denominator equal to 0.

x² - 3x + 2  =  0

(x - 1) (x - 2)  =  0

x  =  1 and x  =  2

Hence R - {1, 2} is the domain of the given function. 

(iii)  √(x - 2)

Solution :

Domain for the radical function means, the values we choose for x must satisfy the condition f(x) ≥ 0

Note : If the radical function is in the denominator, then it must satisfy the condition f(x) > 0.

x - 2 ≥ 0

x  ≥  2

Hence the required domain is [2, ∞).

(iv)  Find the domain of the function f(x) defined by f(x)  =  √(4 - x) + (1/√(x² - 1))

Solution :

f(x)  =  √(4 - x) + (1/√(x² - 1))

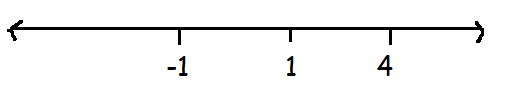
By selecting a value lesser than -1, √(4-x) and √(x²-1) will become greater than 0.

By selecting a value greater than 1, √(x²-1) will become greater than 0. By choosing a value greater than 4, √(4-x) will become lesser than 0.

By combining the intervals, we get

Domain (f)  =  (-∞, -1) U (1, 4]

(v)  (2x + 1)/(x² - 9)

Solution :

f(x)  =  (2x + 1)/(x² - 9)

f(x)  =  (2x + 1)/(x + 3)(x - 3)

(x + 3)(x - 3)  =  0

x  =  -3 and x  =  3

Domain of f(x) is R - [-3, 3].

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.