FINDING EQUATION OF LINE FROM GRAPH WORKSHEET

Find equation of the line from the following graph given :

Problem 1  :

Problem 2 :

Problem 3 :

Problem 4 :

Problem 5 :

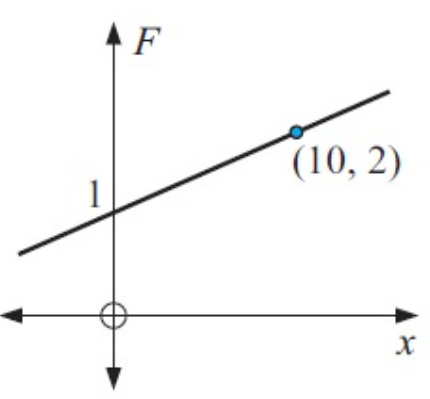
Problem 6 :

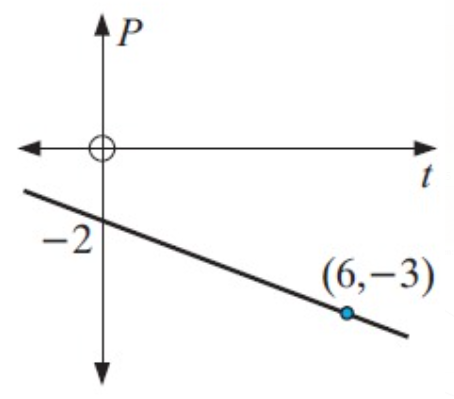
Problem 7 :

Jamila plans to invest $300 by buying shares of two different stock A costs $5.62 per share and Stock B costs $12.97 per share. Which equation represent the number of shares of these stocks Jamila can buy, where a is the number of shares of Stock A and b is the number of shares in stock B ?

a)  12.97a + 5.26b = 300        b) 12.97a - 5.26b = 300

c)  5.62a + 12.97b = 300     d)  5.62a - 12.97b = 300

Problem 8 :

The graph shows the relationship between the number of shares of stock from Company A, x and the number of shares of stock from Company B, y that Simeone can purchase, Which equation could represent this relationship ?

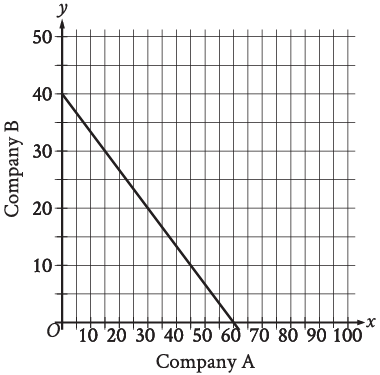
a)  y = 8x + 12     b)  8x + 12y = 480

c)  y = 12x + 8      d)  12x + 8y = 480

Problem 9 :

The graph of the line in the xy-plane has slope 2 and contains the point (1, 8). The graph of the second line passes through the points (1, 2) and (2, 1). If two lines intersect at the point (a, b) what is the value of a + b?

1. Solution :

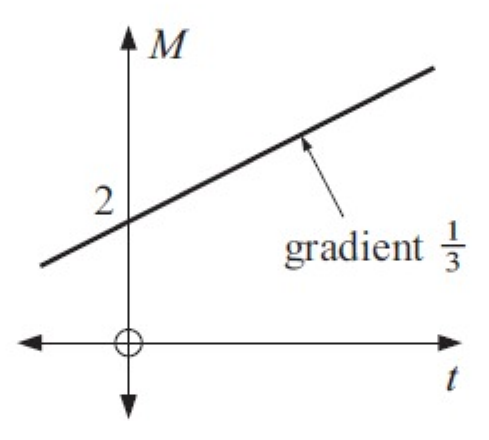
Slope of a line  =  1/3

y – intercept(b)  =  2

Equation of a straight line y  =  mx + b

y  =  1/3x + 2

3y  =  x + 6

x – 3y + 6  =  0

So, the required equation is x – 3y + 6  =  0.

2. Solution :

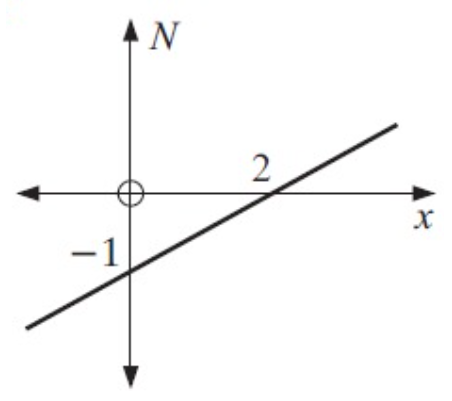
x – intercept form a  =  2

N – intercept form b  =  -1

By using x – intercept and y – intercept formula,

x/a + y/b  =  1

x/2 + N/(-1)  =  1

x/2 – N/1  =  1

- N  =  - 1/2x + 1

N  =  (1/2)x - 1

So, the required equation is N  =  (1/2)x - 1

3. Solution  :

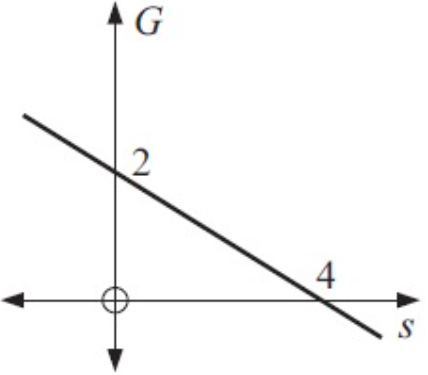
s – intercept form a  =  4

G – intercept form b  =  2

By using x – intercept and y – intercept formula,

x/a + y/b  =  1

S/4 + G/2  =  1

G/2  =  - S/4 + 1

G  =  - S/2 + 2

G  =  (-1/2)S + 2

So, the required equation is G  =  (-1/2)S + 2

4. Solution :

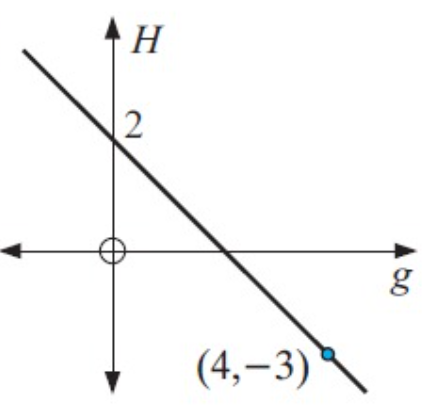
In figure, the straight line passes through two points (4, -3) and (0, 2)

By using two points formula,

(y – y₁)/(y₂ – y₁)  =  (x – x₁)/(x₂ – x₁)

We have two points (4, -3) and (0, 2)

(4, -3)----->(x₁, y₁)

(0, 2)----->(x₂, y₂)

By applying the values, we get

(H+3)/(2+3)  =  (g–4)/(0–4)

(H+3)/5  =  (g–4)/(-4)

(-4) (H+3)  =  5 (g–4)

- 4H–12  =  5g–20

- 4H  =  5g–20+12

- 4H  =  5g–8

H  =  (-5/4)g + 2

So, the required equation is H  =  (-5/4)g + 2

5. Solution :

In figure, the straight line passes through two points (10, 2) and (0, 1)

By using two points formula,

(y – y₁)/(y₂ – y₁)  =  (x – x₁)/(x₂ – x₁)

We have two points (10, 2) and (0, 1)

(10, 2)------>(x₁, y₁)

(0, 1)------>(x₂, y₂)

By applying the values, we get

(F–2)/(1–2)  =  (x–10)/(0-10)

(F–2)/(-1)  =  (x–10)/(-10)

(-10) (F–2)  =  (-1) (x–10)

-10F+20  =  - x+10

- 10F  =  - x+10–20

- 10F  =  -x–10

F  =  (1/10)x + 1

So, the required equation is F  =  (1/10)x + 1

6. Solution :

In figure, the straight line passes through two points (6, -3) and (0, -2)

By using two points formula,

(y – y₁)/(y₂ – y₁)  =  (x – x₁)/(x₂ – x₁)

We have two points (6, -3) and (0, -2)

(6, -3)------>(x₁, y₁)

(0, -2)------>(x₂, y₂)

By applying the values, we get

(P+3)/(-2+3)  =  (t–6)/(0–6)

(P+3)/1  =  (t–6)/(-6)

(-6) (P+3)  =  t–6

- 6P–18  =  t–6

- 6P  =  t–6+18

- 6P  =  t+12

P  =  (-1/6)t - 2

So, the required equation is P  =  (-1/6)t – 2

7. Solution :

a - number of shares of stock A

b - number of shares of stock B

5.62 a + 12.97 b = 300

8. Solution :

From the y-intercept, run = 60 and rise = -40

One of the points on the graph (45, 10)

y = mx + b

slope = rise/run

= -40/60

= -2/3

y - y₁ = m(x - x₁)

y - 10 = (-2/3)(x - 45)

3(y - 10) = -2(x - 45)

3y - 30 = -2x + 90

2x + 3y = 90 + 30

2x + 3y = 120

Multiplying the equation by 4, we get

8x + 12y = 480

So, option b is correct.

9. Solution :

Equation of first line :

Slope = 2 and point (1, 8)

y - y₁ = m(x - x₁)

y - 8 = 2(x - 1)

y = 2x - 2 + 8

y = 2x + 6 ------(1)

Equation of second line :

(1, 2) and (2, 1)

Slope = (y₂ - y₁)/(x₂ - x₁)

= (1 - 2) / (2 - 1)

= -1/1

m = -1

(y - 2) = -1(x - 1)

y - 2 = -x + 1

y = -x + 1 + 2

y = -x + 3 ------(2)

Solving (1) and (2), we get

y = y 

2x + 6 = -x + 3

2x + x = 3 - 6

3x = -3

x = -1

applying x = -1, we get

y = -(-1) + 3

y = 1 + 3

y = 4

So, the point of intersection is at (-1, 4)

a = -1 and b = 4

a + b = -1 + 4

= 3

So, the value of a + b is 3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.