FINDING EXPONENTIAL FUNCTIONS FROM A TABLE

Definition of Exponential Function :

Let a and b be real number constants. An exponential function in x is a function that can be written in the form

f(x)  =  a ⋅ b^x

where a is nonzero, b is positive and b ≠ 1.

The constant a is the initial value of f (the value x =  0) and b is the base.

Let us see some examples to understand how to form a exponential function from the table.

Example 1 :

Determine the formulas for the exponential functions g and h whose values are given in the following table.

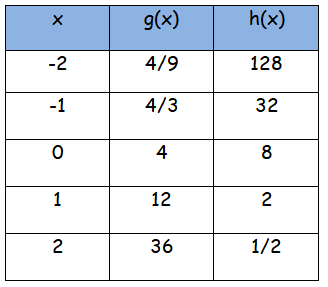
Solution :

Finding function g(x) :

General form of the exponential function is f(x)  =  a ⋅ b^x

g(x)  =  a ⋅ b^x  -----(1)

By applying the values of a and b in the general form of exponential function, we get

g(x)  =  4 ⋅ 3^x

Finding function h(x) :

h(x)  =  a ⋅ b^x  -----(2)

By applying the values of a and b in the general form of exponential function, we get

h(x)  =  8 ⋅ (1/4)^x

Example 2 :

Determine the formulas for the exponential functions g and h whose values are given in the following table.

Solution :

Finding function f(x) :

General form of the exponential function is f(x)  =  a ⋅ b^x

g(x)  =  a ⋅ b^x  -----(1)

By applying the values of a and b in the general form of exponential function, we get

f(x)  =  (3/2) ⋅ (1/2)^x

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.