FINDING GRADIENT AND Y-INTERCEPT FROM AN EQUATION

Find the gradient and y intercept of the line with equation :

Problem 1 :

2x + 3y  =  8

Solution :

Given equation is, 2x + 3y  =  8

3y  =  -2x + 8

y  =  (-2x/3) + 8/3

Gradient (m)  =  (-2/3)

y – intercept (b)  =  (8/3) 

Problem 2 :

3x – 7y  =  11

Solution :

Given equation is, 3x – 7y  =  11

-7y  =  -3x + 11

-y  =  (-3x/7) + 11/7

y  =  (3x/7) + 11/7

Gradient (m)  =  3/7

y – intercept (b)  =  11/7

Problem 3 :

6x – 11y  = 4

Solution :

Given equation is, 6x – 11y  = 4

-11y  =  -6x + 4

-y  =  (-6x/11) + 4/11

y  =  6x/11 + 4/11

Gradient (m)  =  6/11

y – intercept (b)  =  4/11

Problem 4 :

5x + 6y =  -1

Solution :

Given equation is, 5x + 6y =  -1

6y  =  -5x – 1

y  =  (-5x/6) – (1/6)

Gradient (m)  =  -5/6

y – intercept (b)  =  -1/6  

Problem 5 :

3x + 6y  =  -1

Solution :

Given equation is, 3x + 6y  =  -1

6y  =  -3x – 1

y  =  (-3x/6) – (1/6)

y  =  (-1x/2) – (1/6)

Gradient (m)  =  -1/2

y – intercept (b)  =  -1/6 

Problem 6 :

15x – 5y  =  17

Solution :

Given equation is, 15x – 5y  =  17

-5y  =  -15x + 17

-y  =  (-15x/5) + 17/5

y  =  (15x/5) + 17/5

y  =  3x + 17/5

Gradient (m)  =  3

y – intercept (b)  =  17/5 

Problem 7 :

In 2005, 120 students at Lincoln High School had smart phones. By 2010, 345 students in the same school had smart phones. Which of the following best describes the annual rate of change in the number of smart phones students had from 2005 to 2010 at Lincoln High School?

A) The average increase in the number of smart phones per year is 40.

B) The average increase in the number of smart phones per year is 45.

C) The average increase in the number of smart phones per year is 50.

D) The average increase in the number of smart phones per year is 55

Solution :

Let x be the year and y be the number of smart phones.

Writing this relationship as ordered pairs, we get

(2005, 120) and (2010, 345)

Slope = (345 - 120) / (2010 - 2005)

= 225 / 5

= 45

B) The average increase in the number of smart phones per year is 45 is the correct answer.

Problem 8 :

The line in the xy-plane has a slope of 9 and passes through the point (0, -5). The equation y = px + r defines the line, where p and r are constants. What is the value of p ? 

Solution :

y = px + r

The given equation is in the form of y = mx + b

Here m = p = 9 and passes through the point (0, -5).

y = 9x + r ----(1)

-5 = 9(0) + r

r = -5

Applying the value of r in (1), we get

y = 9x - 5

Problem 9 :

The table shows three values of x and their corresponding values of y, where s is a constant. There is a linear relationship between x and y. Which of the following equations represents this relationship?

A) sx + 3y = 18s     B) 3x + sy = 18s

C) 3x + sy = 18       D) sx + 3y = 18

Solution :

(-2s, 24) and (-s, 21)

Slope = (21 - 24) / (-s - (-2s))

= -3/(-s + 2s)

Slope = -3/s

y = mx + b

Here slope m = -3/s and to find the y-intercept, we have to apply the another point in the equation above.

y = (-3/s) x + b -----(1)

(s, 15)

15 = (-3/s) s + b

15 = -3 + b

b = 15 + 3

b = 18

Applying the value of b in (1), we get

y = (-3/s) x + 18

y = (-3x + 18)/s

sy = -3x + 18

3x + sy = 18 is the required equation.

Problem 10 :

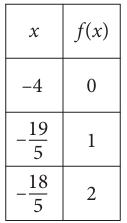
For the linear function, f the table shows three values of x and their corresponding values of f(x). If h(x) = f(x) - 13, which equation defines h ?

a)  h(x) = 5x - 4         b)  h(x) = 5x + 7

c)  h(x) = 5x + 9       d) h(x) = 5x + 20

Solution :

The linear function h(x) will be in the form of y = mx + b.

(-4, 0) and (-19/5, 1)

Slope m = (1 - 0) / (-19/5 + 4)

= 1 / (-19 + 20)/5

= 1/1/5

= 5

y = 5x + b ----(1)

Applying the point (-18/5, 2), we get

2 = 5(-18/5) + b

2 = -18 + b

b = 18 + 2

b = 20

By applying the value of b in (1), we get

y = 5x + 20

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.