FINDING INCREASING AND DECREASING INTERVALS FROM A GRAPH

Find intervals where f(x) is 

(a)  increasing  (b)  decreasing

Example 1 :

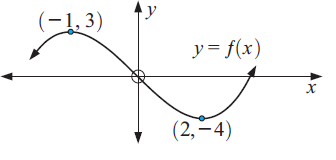
Solution :

By analyzing the graph, we get

(a)  f(x) is increasing for x ≤ -1 and for x ≥ 2

(b)  f(x) is decreasing for -1 ≤ x ≤ 2

Example 2 :

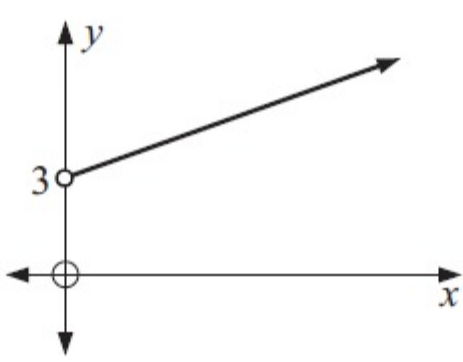
Solution :

The function is

(i)  increasing for x > 0 and 

(ii)  it is not decreasing.

Example 3 :

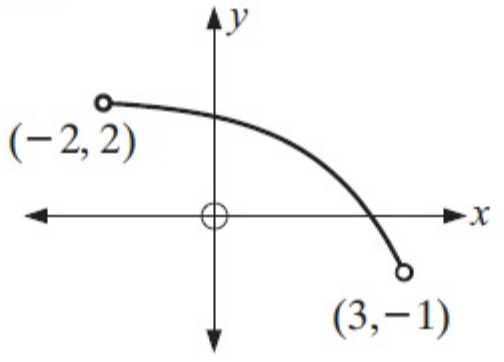
Solution :

The function is

(i)  It is not increasing.

(ii)  decreasing for -2 < x < 3

Example 4 :

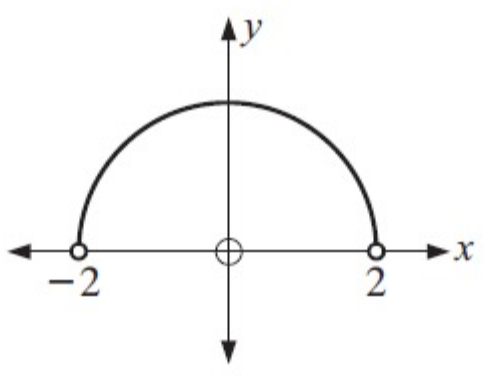
Solution :

The function is

(i)  increasing for -2 < x < 0 and

(ii)  decreasing for 0 < x < 2.

Example 5 :

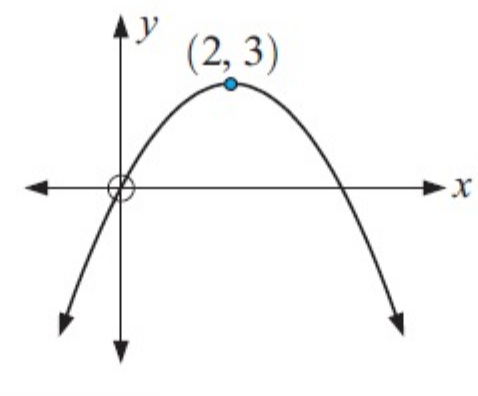
Solution :

The function is

(i)  increasing for x < 2 and

(ii)  decreasing for x > 2.

Example 6 :

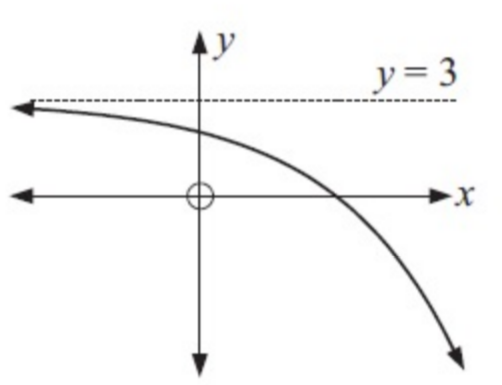
Solution :

The horizontal asymptote shows that the function approaches as x tends to +∞ or −∞. 

The function is

(i)  never increase

(ii)  decreasing for all x.

Example 7 :

Solution :

The function is

(i)  increasing for all x

(ii)  not decreasing.

Example 8 :

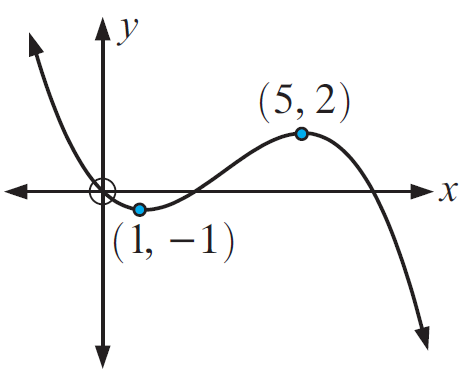
Solution :

(i)  Increasing at 1 < x < 5

(ii)  decreasing at x < 1 and x > 5

Example 9 :

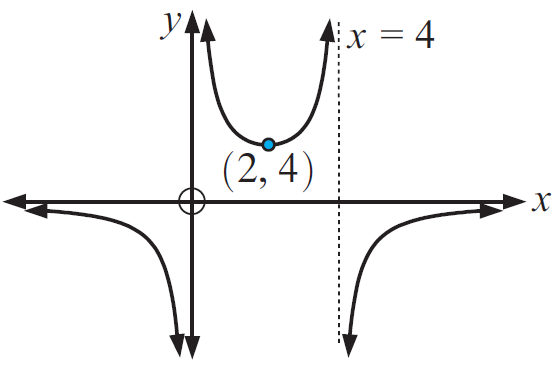
Solution :

(i)  increasing 2 < x < 4 (since we have vertical asymptote at x = 4).

(ii)  decreasing at 0 < x < 2.

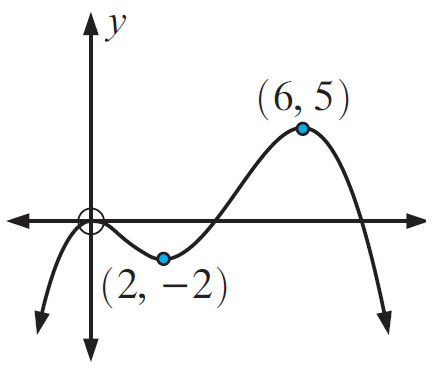
Solution :

(i)  increasing x < 0 and 2 < x < 6

(ii) decreasing 0 < x < 2 and x > 6.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.