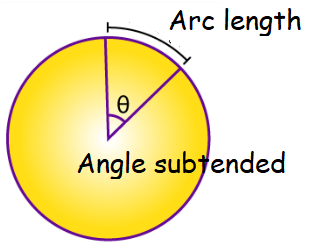
FINDING LENGTH OF ARC WITH ANGLE AND RADIUS

Length of arc  =  (θ/360) ⋅ 2πr

here θ  -  angle formed by two radius

r  -  radius

Example 1 :

Find the length of arc whose radius is 42 cm and central angle is 60°

Solution :

Length of arc  =  (θ/360) x 2πr

Here central angle (θ)  =  60° and radius (r)  =  42 cm

  =  (60°/360) ⋅ 2 ⋅ (22/7) ⋅ 42

  =  (1/6) ⋅ 2 ⋅ 22 ⋅ 6

  =  2 ⋅ 22

  =  44 cm

Example 2 :

Find the length of arc whose radius is 10.5 cm and central angle is 36°

Solution :

Length of arc = (θ/360) x 2πr

Here central angle (θ) = 36° and radius (r) = 10.5 cm

  =  (36°/360) ⋅ 2 ⋅ (22/7) ⋅ 10.5

  =  (1/10) ⋅ 2 ⋅ (22/7) ⋅ 10.5

  =  (1/5) ⋅ (22/7) ⋅ 10.5

  =  (22/7) ⋅ 2.1

  =  22 ⋅ 0.3

  =  6.6 cm

Example 3 :

Find the length of arc whose radius is 21 cm and central angle is 120°

Solution :

Length of arc  =  (θ/360) ⋅ 2πr

Here central angle (θ)  =  120° and radius (r) = 21 cm

  =  (120°/360) ⋅ 2 ⋅ (22/7) ⋅ 21

  =  (1/3) ⋅ 2 ⋅ 22 ⋅ 3

  =  2 ⋅ 22

  =  44 cm

Example 4 :

Find the length of arc whose radius is 14 cm and central angle is 5°

Solution :

Length of arc = (θ/360) x 2πr

Here central angle (θ) = 5° and radius (r) = 14 cm

  =  (5°/360) ⋅ 2 ⋅ (22/7) ⋅ 14

  =  (1/72) ⋅ 2 ⋅ 22 ⋅ 2

  =  (1/36) ⋅ 2 ⋅ 22

  =  (1/18) ⋅ 22

  =  (1/9) ⋅ 11

  =  11/9

  =  1.22 cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.