FINDING LENGTH OF DIAGONAL OF A RECTANGLE

A rectangle is a special case of a parallelogram in which each pair of adjacent sides is perpendicular. 

Diagonals will divide the rectangle into two right triangles.

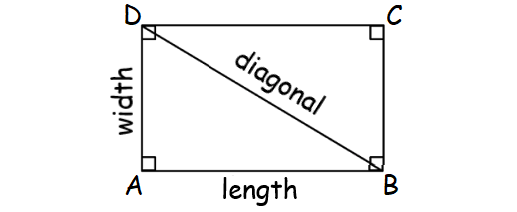
We can find the length of diagonal BD in the rectangle ABCD above using Pythagorean Theorem in the right ΔABD.

In the right ΔABD, by Pythagorean Theorem,

BD² = AB² + AD²

Take square root on both sides.

Example 1 :

A rectangle has sides of length 8 cm and 3 cm. Find the length of each diagonal.

Solution :

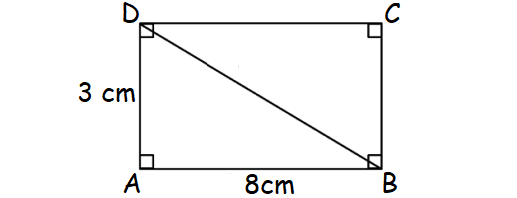
In the rectangle ABCD above, AB = 8 cm and AD = 3 cm.

In the right ΔABD, by Pythagorean Theorem,

BD² = AB² + AD²

BD² = 8² + 3²

BD² = 64 + 9

DB² = 73

Take square root on both sides.

DB = √73

The length of each diagonal is √73 cm.

Example 2 :

The length of a rectangle is three times of its width. If the diagonal is 10 cm long, find the length and width of the rectangle.

Solution :

Let x be width of the rectangle.

Then, the length = 3x

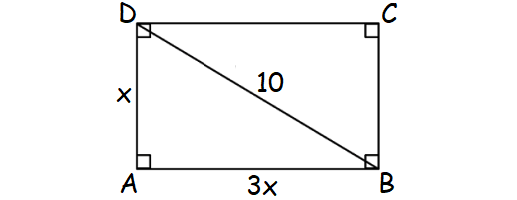
In the right ΔABD, by Pythagorean Theorem,

AB² + AD² = BD²

(3x)² + x² = 10²

9x² + x² = 100

10x² = 100

Divide both sides by 10.

x² = 10

Take square root on both sides.

x = √10

width = √10 cm

length = 3√10 cm

Example 3 :

The length and width of a rectangle are in the ratio 2 : 1. If the diagonal is 10 cm long, find the perimeter and area area of the rectangle.

Solution :

From the ratio 2 : 1, length and width of the rectangle can be assumed as 2x and 1x.

By Pythagorean theorem,

(2x)² + x² = 10²

4x² + x² = 100

5x² = 100

Divide both sides by 5.

x² = 20

Take square root on both sides.

x = √20

x = 2√5

length = 2(2√5) = 4√5

width = 2√5

Perimeter of the rectangle :

= 2(l + w)

= 2(4√5 + 2√5)

= 2(6√5)

= 12√5 cm

Area of the rectangle :

= length x width 

= 4√5(2√5)

= 8(5)

= 40 cm²

Example 4 :

The width of a rectangular field is 60% of its length. If the perimeter of the field is 800 m, find the length of its diagonal (Round your answer to the nearest whole number, if required).

Solution :

Let x be the length.

Then, the width = 60% of x = 0.6x.

Perimeter of the rectangle = 800 m

2(x + 0.6x) = 800

2(1.6x) = 800

3.2x = 800

Divide both sides by 3.2.

x = 250

length = 250 m

width = 0.6(250) = 150 m

By Pythagorean Theorem,

(diagonal)²  =  (length² + (width)²

(diagonal)² = 250² + 150²

(diagonal)² = 625000 + 22500

(diagonal)² = 85000

Take square root on both sides.

diagonal = √85000

diagonal ≈ 292

Length of the diagonal is about 292 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.