FINDING LOCAL EXTREMA WITH SECOND DERIVATIVE TEST

The Second Derivative Test relates the concepts of critical points, extreme values, and concavity to give a very useful tool for determining whether a critical point on the graph of a function is a relative minimum or maximum. 

Find the local extrema for the following functions using second derivative test :

Problem 1 :

f(x) = −3x⁵+ 5x³

Solution :

f(x) = −3x⁵+ 5x³

f'(x)  =  -15x⁴ + 15x²

f'(x)  =  0

-15x²(x² - 1)  =  0

x  =  0 and x² - 1  =  0

x  =  0, 1 and -1

f''(x)  =  -20x³+30x

f''(0)  =  -20(0)³+30(0)  ==>  0

f''(1)  =  -20(1)³+30(1)  ==>  10 > 0 (local minimum)

f''(-1)  =  -20(-1)³+30(-1)  ==>  -10 < 0 (local maximum)

So, local maximum at x  =  -1.

Maximum value :

f(-1)  =   −3(-1)⁵+ 5(-1)³

f(-1)  =   3 - 5  ==>  -2

So, local maximum point is (-1, -2) and local maximum is -2.

So, local minimum at x  =  1.

Minimum value :

f(1)  =   −3(1)⁵+ 5(1)³

f(1)  =   -3 + 5  ==>  2

So, local maximum point is (1, 2) and local maximum is 2.

Problem 2 :

f(x)  =  x logx

Solution :

f(x)  =  x logx

f'(x)  =  x(1/x) + log x (1)

f'(x)  =  1 + log x

f'(x)  =  0

1 + log x  =  0

log x  =  -1

x  =  e^-1

x  =  1/e

f''(x)  =  0 + 1/x

f''(x)  =  1/x

f''(1/e)  =  e > 0 (local minimum)

Local minimum at x  =  1/e

f(1/e)  =  (1/e) log (1/e)

f(1/e)  =  (1/e) log (e^-1)

f(1/e)  =  (1/e) (-1)

f(1/e)  =  -1/e

So, local minimum is -1/e

Problem 3 :

f(x)  =  x²e^-2x 

Solution :

f(x)  =  x²e^-2x 

f'(x)  =  x²(-2e^-2x) + e^-2x(2x)

e^-2x (-2x²+2x)  =  0

e^-2x (x-x²)  =  0

x(1-x)  =  0

x  =  0 and x  =  1

f''(x)  =  x(-1) + (1-x)(1)

f''(x)  =  -x + 1-x

f''(x)  =  1-2x

f''(0)  =  1 > 0 (Local minimum)

f''(1)  =  -1 (Local maximum)

Local maximum  =  1/e²

Local minimum  =  0

Problem 4 :

For the function

f(x)  =  4x³+3x²-6x+1

find the intervals of 

(i)  monotonicity

(ii)  local extrema

(iii)  intervals of concavity and

(iv)  points of inflection.

Solution :

f(x)  =  4x³+3x²-6x+1

f'(x)  =  12x²+6x-6

f'(x)  =  0

12x²+6x-6  =  0

6(2x²+x-1)  =  0

(2x-1)(x+1)  =  0

x  =  1/2 and x  =  -1

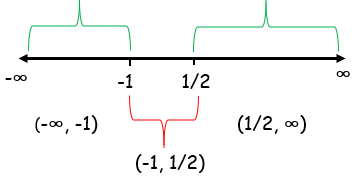
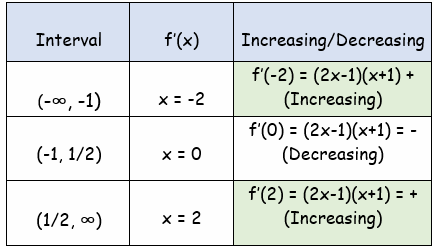
The function is increasing on (-∞, -1) and (1/2, ∞), it is decreasing on (-1, 1/2).

f'(x)  =  (2x²+x-1) 

f''(x)  =  4x + 1

f''(x)  =  0

x  =  -1/4

 (-∞, -1/4)  and (-1/4, ∞) 

From  (-∞, -1/4), we take -2

f''(-2)  =  -7 < 0 (Local maximum)

Concave downward on (-∞, -1/4).

From (-1/4, ∞) , we take 2

f''(2)  =  9 < 0 (Local minimum)

Concave upward on (-1/4, ∞).

At -2 it changes from negative to positive, then it turns into maximum to minimum.

Local maximum :

x  =  -1

f(-1)  =  4(-1)³+3(-1)²-6(-1)+1

=  -4+3+6+1

=  6

Local minimum :

x  =  1/2

f(1/2)  =  4(1/2)³+3(1/2)²-6(1/2)+1

=  (1/2)+(3/4)-3+1

=  (2+3-8)/4

=  -3/4

Point of inflection :

f(1/4)  =  4(-1/4)³+3(-1/4)²-6(-1/4)+1

=  -1/16 + 3/16 + 6/4 + 1

=  (-1+3+24+16)/16

=  42/16

=  21/8

Point of inflection is (-1/4, 21/8)

Problem 5 :

f(x) = (1/2)x + sin x defined in the closed interval [0, π] has a critical point at x = 

a)  2π/3       b)  π/3     c)  π      d)  5π/6         e)  0

Solution :

f(x) = (1/2)x + sin x

To find critical point, we have to equate f'(x) to 0 and solve for x.

f'(x) = (1/2)(1) + cos x

f'(x) = (1/2) + cos x

f'(x) = 0

(1/2) + cos x = 0

cos x = -1/2

x = cos^-1(-1/2)

 π -  π/3

= 2 π/3

So, the required critical point is 2 π/3.

Problem 6 :

the function is defined by g(x) = 4x³ - 3x² for all real values of x has a relative maximum at x =

a)  -1/2     b)  0     c)  1/2    d)  1/4    e)  1

Solution :

g(x) = 4x³ - 3x²

g'(x) = 4(3x²) - 3(2x)

= 6x² - 6x

g'(x) = 0

6x² - 6x = 0

6x(x - 1) = 0

x = 0 and x = 1

Finding the second derivative :

g''(x) = 6(2x) - 6(1)

= 12x - 6

When x = 0

g''(0) = 12(0) - 6

= -6 < 0 Maximum

When x = 1

g''(1) = 12(1) - 6

= 6 > 0 Minimum

So, relative maximum at x = 0, option b is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.