FINDING MEASUREMENTS OF A TRIANGLE

Example 1 :

Find the area and perimeter of the triangle shown below. 

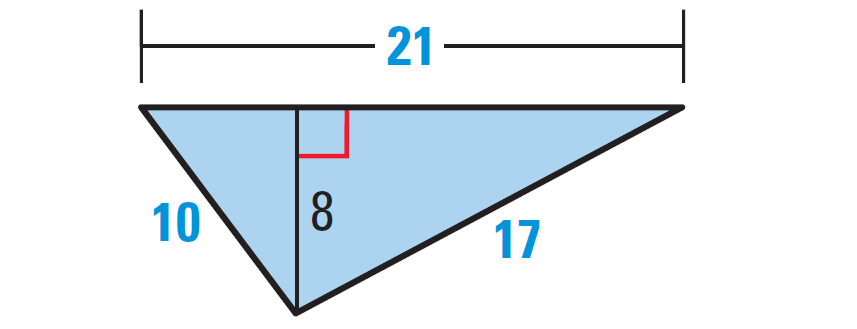
Solution : 

Because we want to find the area of the triangle, we have to know its base and height. 

To know the base and height of the triangle, let us rotate the given triangle as shown below. 

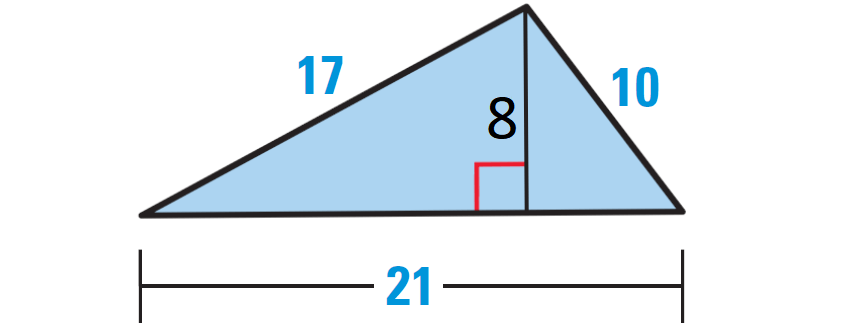
Base = 21 units and height = 8 units. 

Area of the triangle :

=  (1/2)⋅ base ⋅ height

 =  (1/2) ⋅ 21 ⋅ 8

=  84 square units

Perimeter of the triangle :

=  Sum of the lengths of all the three sides

=  17 + 10 + 21

=  48 units 

Example 2 :

Find the area and perimeter of the triangle given below. 

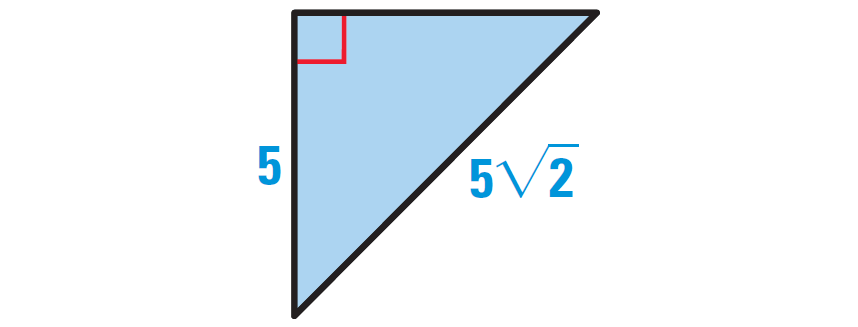
Solution : 

Because we want to find the area of the triangle, we have to know its base and height. 

To know the base and height of the triangle, let us rotate the given triangle as shown below. 

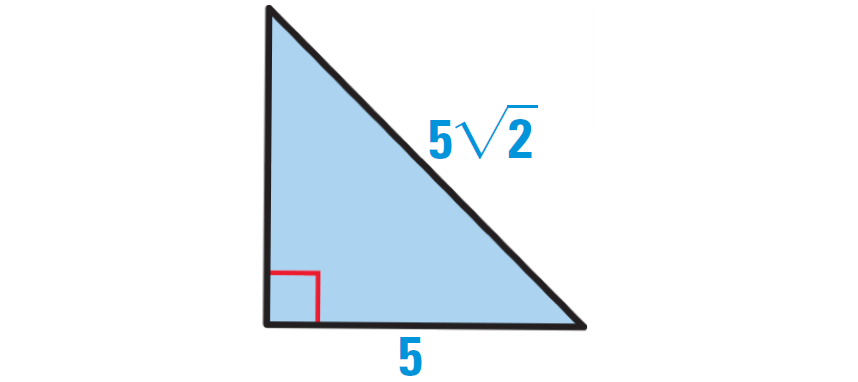
Use Pythagorean theorem to find the height of the triangle.

h² + 5²  =  (5√2)²

h² + 25  =  5² ⋅ (√2)²

h² + 25  =  25 ⋅ 2

h² + 25  =  50

Subtract 25 from each side. 

h²  =  25

h²  =  5²

h  =  5

Area of the triangle : 

=  (1/2) ⋅ base ⋅ height

=  (1/2) ⋅ 5 ⋅ 5

=  12.5 square units

Perimeter of the triangle :

=  Sum of the lengths of all the three sides

=  5 + 5 + 5√2

=  (10 + 5√2) units

Example 3 :

Area of the triangle shown below is 126 square units. Find the perimeter and height of the triangle. 

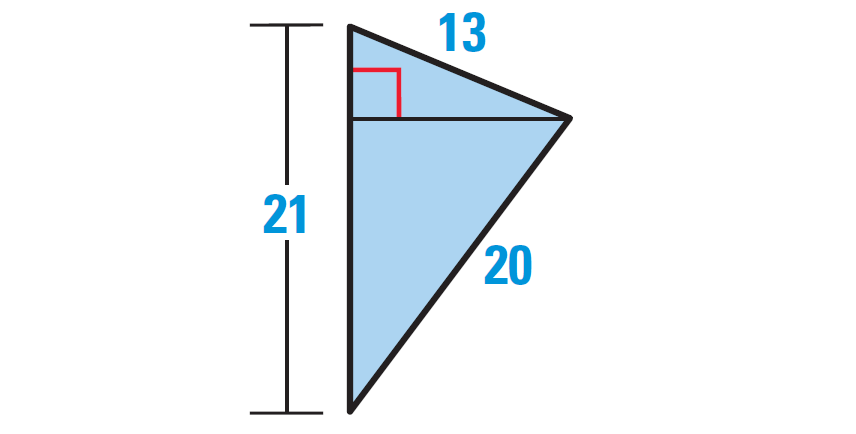
For our convenience, let us rotate the given triangle as shown below. 

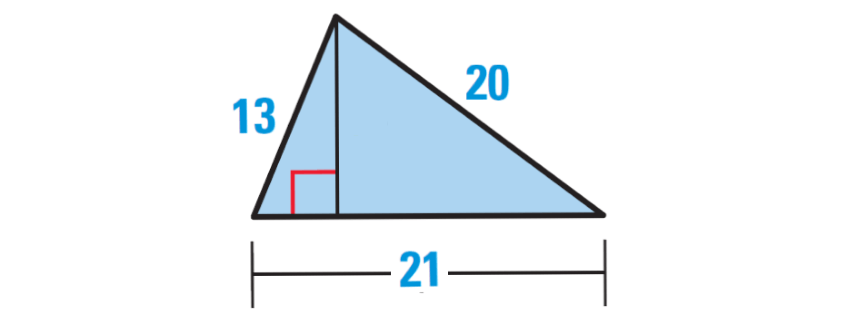
In the triangle above, base = 21 units.

Given :

Area of the triangle  =  126 square units

(1/2) ⋅ base ⋅ height  =  126

Substitute base = 21.

(1/2) ⋅ 21 ⋅ height  =  126

Multiply each side by 2.

21 ⋅ height  =  126⋅2

21 ⋅ height  =  252

Divide each side by 21.

(21 ⋅ height)/21  =  252/21

height  =  12

Perimeter of the triangle : 

=  Sum of the lengths of all the three sides

=  13 + 20 + 21

=  54 units

Example 4 :

Find the area and perimeter of the triangle defined by D(1, 3), E(8, 3) and F(4, 7). 

Solution : 

Plot the points in the coordinate plane. Draw the height from F to the side DE. Label the point where the height meets DE as G. Point G has coordinates (4, 3). 

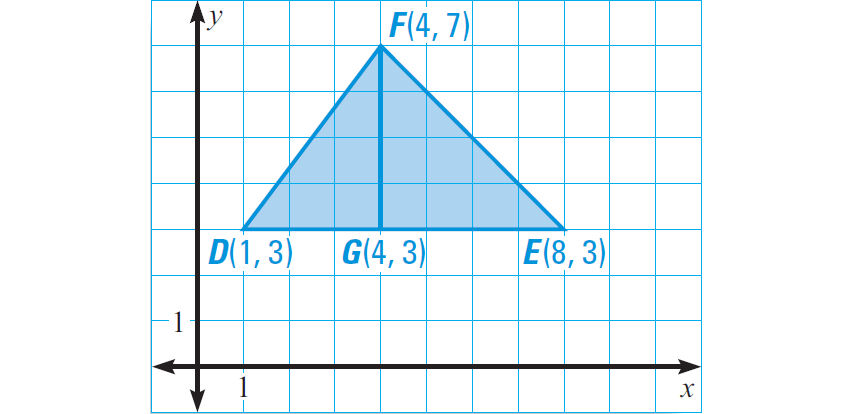
Length of DE : 

=  8 - 1

=  7

Use distance formula to find the length of EF and FD.

Distance Formula :

=  √[(x₂ - x₁)² + (y₂ - y₁)²]

Length of EF : 

(x₁, y₁)  =  E(8, 3)

(x₂, y₂)  =  F(4, 7)

EF  =  √[(4 - 8)² + (7 - 3)²]

EF  =  √[(-4)² + (4)²]

EF  =  √[16 + 16]

EF  =  √32

EF  =  √(4 ⋅ 4 ⋅ 2)

EF  =  4√2

Length of FD : 

(x₁, y₁)  =  F(4, 7)

(x₂, y₂)  =  D(1, 3)

FD  =  √[(1 - 4)² + (3 - 7)²]

FD  =  √[(-3)² + (-4)²]

FD  =  √[9 + 16]

FD  =  √25

FD  =  5

Perimeter of the triangle :

=  5 + 7 + 4√2

=  (12 + 4√2) units

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.