FINDING MISSING ANGLE MEASURES IN TRIANGLES

If we know the measures of two angles in a triangle, we can use the Triangle Sum Theorem to find the measure of the third angle.

Example 1 :

Find the missing angle measure in the triangle given below.

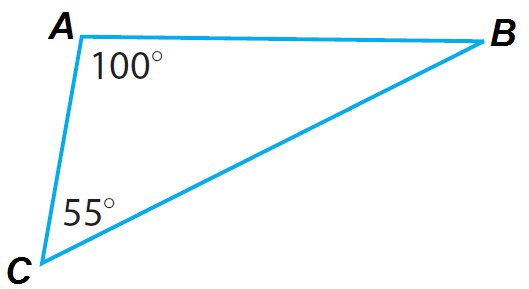
Solution :

Step 1 :

Write the Triangle Sum Theorem for this triangle.

m∠A + m∠B + m∠C  =  180°

Step 2 :

Substitute the given angle measures.

55° + m∠B + 100°  =  180°

Simplify.

m∠B + 155°  =  180°

Subtract 155° from both sides.

m∠B  =  25°

Example 2 :

Find the missing angle measure in the triangle given below.

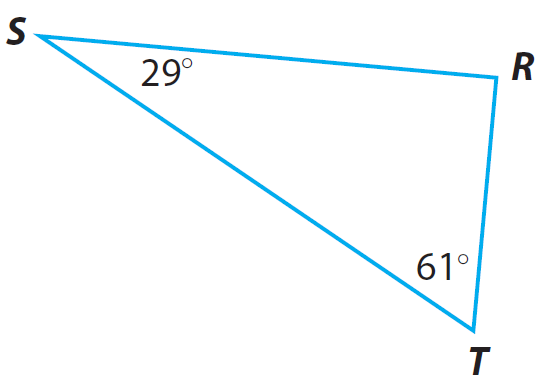
Solution :

Step 1 :

Write the Triangle Sum Theorem for this triangle.

m∠R + m∠S + m∠T  =  180°

Step 2 :

Substitute the given angle measures.

m∠R + 29° + 61°  =  180°

Simplify.

m∠R + 90°  =  180°

Subtract 90° from both sides.

m∠R  =  90°

Example 3 :

Find the missing angle measure in the triangle given below.

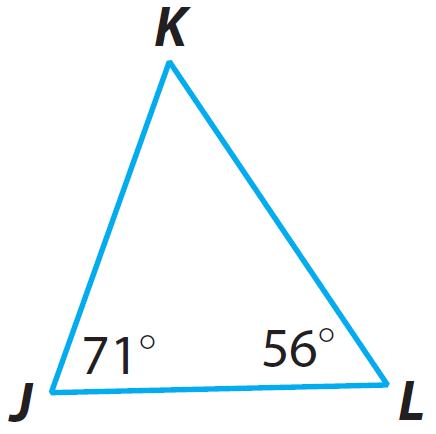
Solution :

Step 1 :

Write the Triangle Sum Theorem for this triangle.

m∠J + m∠K + m∠L  =  180°

Step 2 :

Substitute the given angle measures.

71° + m∠K + 56°  =  180°

Simplify.

m∠K + 127°  =  180°

Subtract 127° from both sides. 

m∠K  =  53°

Example 4 :

Find the measure of each angle in the triangle given below.

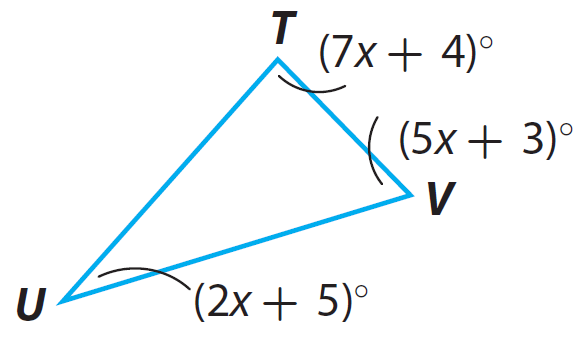
Solution :

Step 1 :

Write the Triangle Sum Theorem for this triangle.

m∠T + m∠U + m∠V  =  180°

Step 2 :

Substitute the given angle measures.

(7x + 4)° + (2x + 5)° + (5x + 3)°  =  180°

Simplify.

14x + 12  =  180

Subtract 12 from both sides.

14x  =  168

Divide both sides by 14.

14x/14  =  168/14

x  =  12

Step 3 :

Substitute x  =  12 in the given angle measures. 

m∠T  =  (7x + 4)°  =  (7 · 12 + 4)°  =  88°

m∠U  =  (2x + 5)°  =  (2 · 12 + 5)°  =  29°

m∠V  =  (5x + 3)°  =  (5 · 12 + 3)°  =  63°

So, 

m∠T  =  88°

m∠U  =  29°

m∠V  =  63°

Example 5 :

In an acute triangle, the measures of two angles are 50° and 60°. What is the measure of the third angle?

Solution :

Let x be the missing angle.

50 + 60 + x = 180

110 + x = 180

x = 180 - 110

x = 70

So, the missing angle is 70 degree.

Example 6 :

In an obtuse triangle, the measures of two angles are 120° and 10°. What is the measure of the third angle?

Solution :

Since it is obtuse triangle, then one of the angle measure would be more than 90 degree and it is given.

Let x be the third angle.

x + 120 + 10 = 180

x + 130 = 180

x = 180 - 130

x = 50

So, the third angle is 50 degree.

Example 7 :

One acute angle of a right triangle measures 35°. What is the measure of the other acute angle?

Solution :

Since it is right angle, one angle measure should be 90°

Let x be the required acute angle.

x + 90 + 35 = 180

x + 125 = 180

x = 180 - 125

x = 55

So, the required angle is 55°.

Example 8 :

If two of the three angles in a triangle have measure 34º and 72º, what is the measure of the third angle?

Solution :

Let x be the third angle.

34 + 72 + x = 180

106 + x = 180

x = 180 - 106

x = 74

So, the third angle is 74º.

Example 9 :

Find the angle measures of a triangle if the second angle measures 10 degrees less than twice the first, and the third angle measures 25 degrees more than the second.

Solution :

Let x be the first angel.

Second angle = 2x - 10

Third angel = 25

x + 25 + 2x - 10 = 180

3x + 15 = 180

3x = 180 - 15

3x = 165

x = 165/3

x = 55

So, the required angle is 55.

Example 10 :

The measure of the second angle is 15 degrees more than the measure of the first angle. The measure of the third angle is 45 degrees more than the measure of the first angle.

Solution :

Let x be the first angel

Second angle = x + 15

Third angle = x + 45

x + x + 15 + x + 45 = 180

3x + 60 = 180

3x = 180 - 60

3x = 120

x = 120/3

x = 40

So, the first angle is 40.

Example 11 :

Find the measures of the interior angles in the triangle. In a triangle ABC, ∠ A = 2X+7, ∠ B = 5X-15, and ∠ C = 6X. What is the value of x?

Solution :

Sum of interior angles of triangle = 180

2x + 7 + 5x - 15 + 6x = 180

13x - 8 = 180

13x = 180 + 8

13x = 188

x = 188/13

x = 14.4

So, the value of x is 14.4.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.