FINDING MISSING ANGLE USING THE CONCEPT OF TRANSVERSAL

Example 1 :

In the figure shown below, if the lines AB an CD are parallel, then find the value of x. 

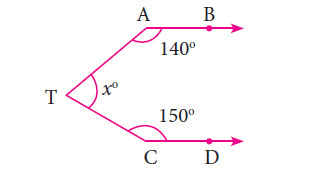
Solution :

Let us draw a line passing through T and parallel to AB and CD.

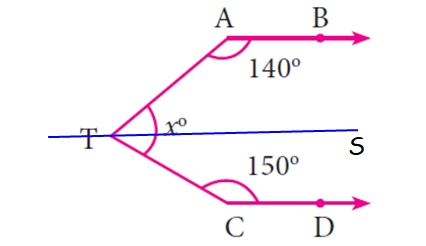
The lines AB and TS are parallel and TA is a transversal.

∠ATS + ∠TAB  =  180°

∠ATS + 140°  =  180

∠ATS  =  180° - 140°  =  40° -----(1)

In a same way 

∠TCD + ∠CTS  =  180°

150° + ∠CTS  =  180°

∠CTS  =  180° - 150°  =  30°  -----(2)

(1) + (2)  ==>  40° + 30°  =  70°

So, the value of x is 70.

Example 2 :

In the figure shown below, if the lines AB an CD are parallel, then find the value of x. 

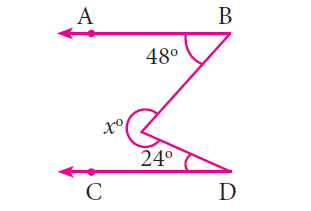
Solution :

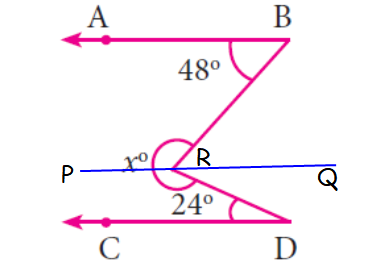
Now we have drawn a line passing through x and it is parallel to AB and CD.

∠PRB + ∠ABR  =  180°

∠PRB + 48  =  180°

∠PRB  =  180° - 48°

∠PRB  =  132° -----(1)

In the same way,

∠PRD + ∠CDR  =  180°

∠PRD + 24°  =  180°

∠PRD  =  180° - 24°  =  156° -----(2)

(1) + (2) ==>  132° + 156°  =  288°

So, the required angle is 288°.

Example 3 :

In the figure shown below, if the lines AB an CD are parallel, then find the value of x. 

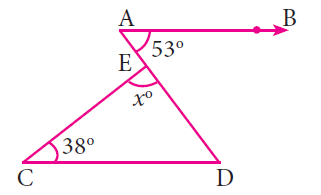
∠BAD  =  ∠ADC (Alternative angles)

∠ADC  =  53°

In triangle ECD,

∠ECD + ∠CDE + ∠DEC  =  180°

38° + 53° + ∠DEC  =  180°

∠DEC  =  180° - 91°

∠DEC  =  89°

So, the value of x is 89.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.