FINDING MISSING COORDINATE GIVEN SLOPE AND TWO POINTS

Find a given that the line joining :

Problem 1 :

A(1, 3) to B(3, a) is parallel to a line with gradient 3.

Solution :

If two lines are parallel, then

Given, A(1, 3) to B(3, a)

Slope m₁  =  (y₂ – y₁)/(x₂ – x₁)

  =  (a -3)/(3 – 1)

  =  (a – 3)/2  ---(1)

Slope of the given line (m₂)  =  3  ---(2)

m₁  =  m₂

(a – 3)/2  =  3

a – 3  =  6

a  =  9

Problem 2 :

P (a, -3) to Q(4, -2) is parallel to a line with gradient 1/3.

Solution :

Given, P (a, -3) to Q(4, -2)

=  (-2 + 3)/(4 – a)

m₁  =  1/(4 – a) ----(1)

m₂  =  1/3  ----(2)

m₁  =  m₂

1/(4 – a)  =  1/3

4 – a  =  3

 – a   =  3 – 4

a  =  1

Problem 3 :

M(3, a) to N(a, 5) is parallel to a line with gradient -2/5.

Solution :

Given, M(3, a) to N(a, 5)

m₁  =  (5 – a)/(a – 3)  ----(1)

m₁  =  m₂

m₂  =  -2/5 ----(2)

-2/5  =  (5 – a)/(a – 3)

-2(a – 3)  =  5(5 – a)

-2a + 6  =  25 - 5a

-2a + 6 – 25 + 5a  =  0

-19 + 3a  =  0

a  =  19/3

a  =  6 1/3

Find t given that the line joining :

Problem 4 :

A(2, -3) to B(-2, t) is perpendicular to a line with gradient 1 1/4.

Solution :

Since two lines are perpendicular then, 

m₁  x  m₂ =  -1

Given, A(2, -3) to B(-2, t)

m₁  =  (y₂ – y₁)/(x₂ – x₁)

=  (t + 3)/(-2 – 2)

=  (t + 3)/-4

m₁ x m₂  =  -1

(t + 3)/-4 x 1 1/4   =  -1

(t + 3)/-4  x  5/4  =  -1

(t + 3) x 5/-16  =  -1

(t + 3) x 5  =  16

5t + 15  =  16

5t  =  16 – 15

5t  =  1

t  =  1/5 

Problem 5 :

C(t, -2) to D(1, 4) is perpendicular to a line with gradient 2/3.

Solution :

Given, C(t, -2) to D(1, 4)

m₁  =  (y₂ – y₁)/(x₂ – x₁)

=  (4 + 2)/(1 – t)

=  6/(1 – t)

m₁ x m₂  =  -1

6/(1 – t)  x  2/3  =  -1

12/3(1 – t)  =  -1

12/3 – 3t  =  -1

12  =  -1 x(3 – 3t)

12  =  -3 + 3t

12 + 3  =  3t

15  =  3t

15/3  =  t

5  =  t

Problem 6 :

The graph of the function f, where y = f (x), models the

total cost y, in dollars, for a certain video game system
and x games. What is the best interpretation of the slope
of the graph in this context?

A) Each game costs $25.

B) The video game system costs $100.

C) The video game system costs $25.

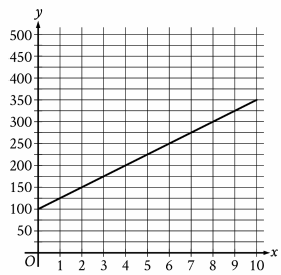
Solution :

By tracing two points from the graph, we get

(1, 125) and (3, 175)

slope m = (175 - 125)/(3 - 1)

= 50/2

= 25

Cost of each game is $25. So, option A is correct.

Problem 7 :

The graph of the linear function f passes through the points (a, 1) and (1, b) in the -xy plane. If the slope of the graph of f is 1, which of the following is true?

a)  a - b = 1      b) a + b = 1       c) a - b = 2

d) a + b = 2

Solution :

Slope of the line passes through the points (a, 1) and (1, b) 

= (b - 1) / (1 - a)

(b - 1) / (1 - a) = 1

b - 1 = 1 - a

b + a = 1 + 1

a + b = 2

So, option d is correct.

Problem 8 :

The line passes through the points (-1, 2) and (5, b) and is parallel to the graph of the equation 4x - 2y = 13. What is the value of b ?

Solution :

When two lines are parallel their slopes will be equal.

Slope of the line joining the points (-1, 2) and (5, b) :

m = (b - 2) / (5 + 1)

m = (b - 2) / 6 -----(1)

Slope of the line 4x - 2y = 13 :

2y = 4x - 13

y = (4x/2) - (13/2)

y = 2x - (13/2)

Slope = 2-----(2)

(1) = (2)

(b - 2) / 6 = 2

b - 2 = 12

b = 12 + 2

b = 14

So, the value of b is 14.

Problem 9 :

Which of the following equations represents a line that passes through (7, 6) and is parallel to the -x-axis?

a)  x = 6       b)  y = 7      c)  y = 7      d)  y = 6

Solution :

When a line is parallel to the x-axis, it must be a perpendicular line.

Perpendicular line will have undefined slope. The perpendicular line which passes through the point (a, b) will in the form of x = a.

So, the required equation is x = 6.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.