FINDING MISSING COORDINATE WHEN THE GIVEN POINTS ARE COLLINEAR

When three points are collinear, and a coordinate is missing in one of the points, we can find the missing coordinate using the area of triangle concept. 

That is, if  three points A(x₁, y₁) B(x₂, y₂) and C(x₃, y₃) will be collinear, then the area of triangle ABC  =  0.

Using the above concept, we can find the missing coordinate in the given points. 

Solved Questions

Question 1 :

Find the value of ‘a’ for which the given points are collinear.

(2, 3), (4, a) and (6, –3)

Solution :

Since the given points are collinear, then area of triangle formed by these points  =  0

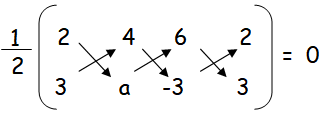
(2a - 12 + 18) - (12 + 6a - 6)  =  0

(2a + 6) - (6 + 6a)  =  0

2a + 6 - 6 - 6a  =  0

-4a  =  0

a  =  0

Question 2 :

Find the value of ‘a’ for which the given points are collinear.

(a, 2 – 2a), (–a + 1, 2a) and (–4–a, 6–2a)

Solution :

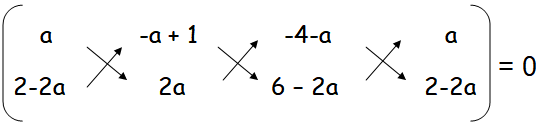
[2a² + (-a + 1)(6 - 2a)+(-4 - a)(2 - 2a)] - [(-a + 1)(2 - 2a)+2a(-4 - a)+a(6 - 2a)]  =  0

[2a² - 6a + 2a² + 6 - 2a - 8 + 8a - 2a + 2a²] - [-2a + 2a² + 2 - 2a - 8a - 2a² + 6a - 2a²]  =  0

(6a² - 2a - 2) - (-2a² - 6a + 2)  =  0

6a² + 2a² - 2a + 6a -2 - 2  =  0

8a² + 4a - 4  =  0

Dividing the entire equation by 4, we get

2a² + a - 1  =  0

(2a - 1) (a + 1)  =  0

a  =  1/2 and a  =  -1

Question 3 :

If the three points (3,-1) , (a, 3) and (1,-3) are collinear, find the value of a.

Solution :

Let the given points be A (3,-1) B (a, 3) and C (1,-3)

Slope of AB  =  (y₂ - y₁)/(x₂ - x₁)

  =  (3-(-1))/(a - 3)

  =  (3 + 1)/(a - 3)

  =  4/(a-3)  ----(1)

Slope of BC  =  (y₂ - y₁)/(x₂ - x₁)

  =  (-3-3)/(1 - a)

  =  -6/(1 - a) ----(2)

Because the given points are collinear, the slopes in (1) and (2) are for the same line. 

So, they are equal. 

(1)  =  (2)

4/(a - 3)  =  -6/(1 - a)

4(1 - a)  =  -6(a - 3)

4 - 4a  =  -6a + 18

6a - 4a  =  18 - 4

2a  =  14

a  =  7

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.