FINDING MISSING SIDE IN SIMILAR TRIANGLES

For the following figures, establish that a pair of triangles is similar, hence find x :

Example 1 :

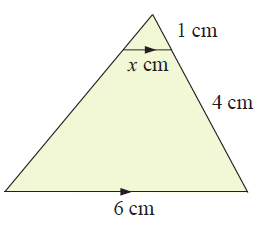
Solution :

Given, DE || BC

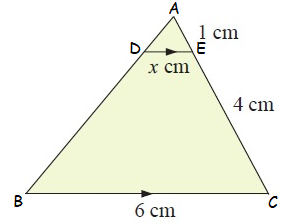Then, DE/BC  =  AE/AC

AE  =  1 cm, AC  =  5 cm, DE  =  x cm, BC  =  6 cm

x/6  =  1/5

x  =  6/5

x  =  1.2

So, the value of x is 1.2 cm

Example 2  :

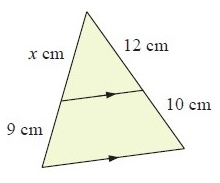
Solution :

Given, DE || BC

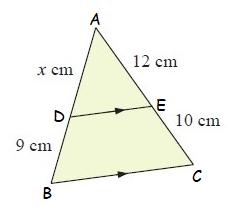Then, AD/DB  =  AE/EC

AD  =  x cm, DB  =  9 cm, AE  =  12 cm, EC  =  10 cm

x/9  =  12/10

x/9  =  6/5

5x  =  54

x  =  54/5

x  =  10.8

So, the value of x is 10.8 cm

Example 3  :

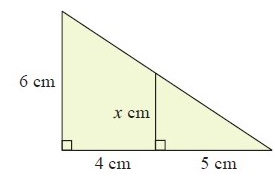
Solution :

By considering the small and larger triangles.

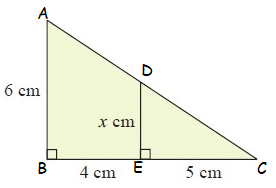Then, DE/AB  =  EC/BC

AB  =  6 cm, DE  =  x cm, EC  =  5 cm, BC  =  9 cm

x/6  =  5/9

x  =  30/9

x  =  10/3

x  =  3 1/3

So, the value of x is 3 1/3 cm

Example 4  :

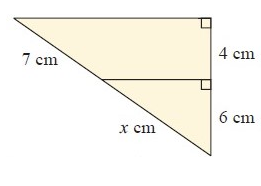
Solution :

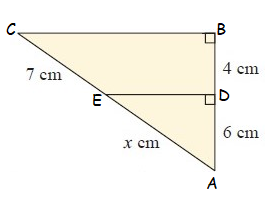EA/CA  =  ED/BC  =  DA/AB

EA/CA  =  DA/AB

x/(7+x)  =  6/(6+4)

x/(7+x)  =  6/10

10x  =  6(7+x)

10x  =  42+6x

4x  =  42

x  =  42/4

x  =  10.5

So, the value of x is 10.5 cm

Example 5  :

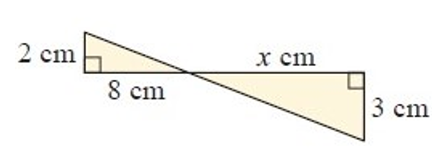
Solution :

In Δ ABC, and ΔCED

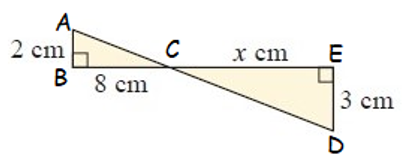
<ACB  =  <ECD  (vertically opposite angles are equal)

<ABC  =  <CED (90 degree)

Using AA theorem, the above triangles Δ ABC ~ ΔCED

AB/ED  =  AC/CD  =  BC/DE

2/3  =  8/x

x  =  8(3)/2

x  =  12 cm

Example 6 :

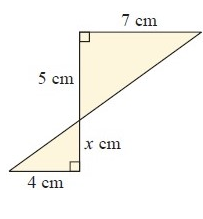
Solution :

In Δ ABC, and ΔCED

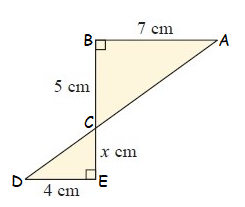Then, DE/AB  =  EC/BC

AB  =  7 cm, BC  =  5 cm, DE  =  4 cm, EC  =  x cm

4/7  =  x/5

x  =  20/7

x  =  2 6/7

So, the value of x is 2 6/7 cm

Example 7 :

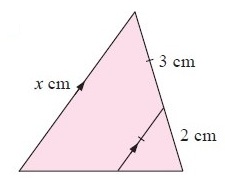
Solution :

In Δ ABC, and ΔAED

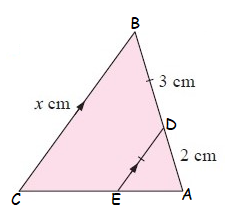
Given, DE || BC

If <ADE  =  <ABC

<EAD  =  <CAB  

So, ∆ADE ~ ∆ABC

Then, DE/BC  =  AD/AB

AD  =  2 cm, AB  =  5 cm, DE  =  3 cm, BC  =  x cm

3/x  =  2/5

2x  =  15

x  =  15/2

x  =  7.5

So, the value of x is 7.5 cm

Example 8 :

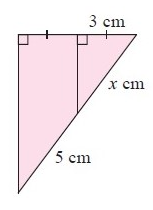
Solution :

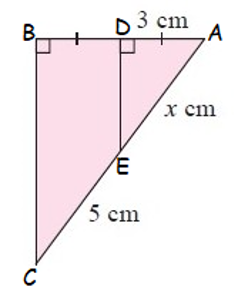
In Δ ADE, and ΔABC

<ADE  =  <ABC  (A)

<DAE  =  <BAC  (A)

So, ∆ADE ~ ∆ABC

AE/AC  =  DE/BC  =  DA/AB

x/(x+5)  =  3/6

x/(x+5)  =  1/2

2x  =  x+5

x  =  5

So, the value of x is 5 cm

Example 9  :

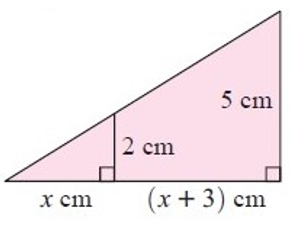
Solution :

In Δ CDE, and ΔABC

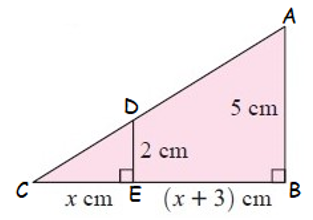
<CED  =  <CBA

<DCE  =  <ACB

So, ∆DEC ~ ∆ABC

Then, DE/AB  =  EC/BC

AB  =  5 cm, DE  =  2 cm, EC  =  x cm, BC  =  2x+3 cm

2/5  =  x/(2x+3)

5x  =  2(2x+3)

5x  =  4x+6

5x – 4x  =  6

x  =  6

So, the value of x is 6 cm.

Example 10 :

a) Find the missing angle in each triangle. How does this show that the triangles are similar?

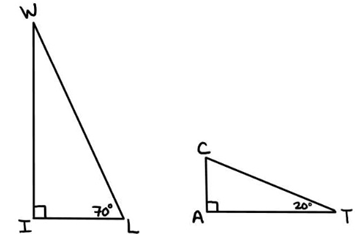
b) If 𝑾𝑰 = 𝟗.𝟒 and 𝑾𝑳 = 𝟏𝟎. Find the side 𝑰𝑳 using the Pythagorean Theorem (to one decimal)

c) If the scale factor from 𝚫𝑾𝑰𝑳 to 𝚫𝑻𝑨𝑪 is ½, find all the missing sides of triangle 𝚫𝑻𝑨𝑪.

Solution :

a)

<WIL = <CAT = 90 degree

<IWL = 180 - (90 + 70)

= 180 - 160

= 20 ----(1)

<WLI = 70

<ACT = 180 - (90 + 20)

= 180 - 110

= 70 ----(2)

<IWL = <ACT = 70 degree

Using AA the triangles WIL and CAT are similar.

By comparing the corresponding sides, we get

b)

𝑾𝑰 = 𝟗.𝟒 and 𝑾𝑳 = 𝟏𝟎

WL² = WI² + IL²

10² = 9.4² + IL²

100 - 88.36 = IL²

IL = √11.64

IL = 3.41

c)

WL/CT = WI/AT = IL/AC = 1/2

Example 11 :

On a sunny day Josée’s shadow is 2.9 m long, while the shadow of a tower is 11.3 m long. If Josée is 1.8 m tall, calculate the height of the tower.

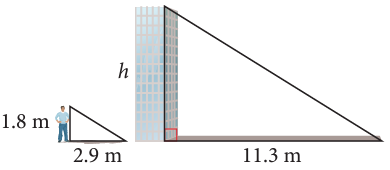
Solution :

Here h is the height of the tower. Since the triangles are similar, we compare the corresponding sides.

1.8/2.9 = h/11.3

Doing cross multiplication, we get

h = 1.8(11.3)/2.9

h = 7

So, the height of the building is 7 m.

Example 12 :

To measure the height of a tree, Cynthia has her little brother, BR, stand so that the tip of his shadow coincides with the tip of the tree’s shadow, at point C

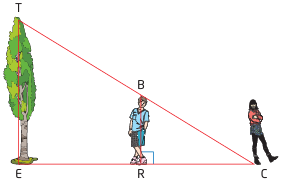
Cynthia’s brother, who is 1.2 m tall, is 4.2 m from Cynthia, who is standing at C, and 6.5 m from the base of the tree. Find the height of the tree, TE.

Solution :

Considering the triangles, TEC and BRC

BR/TE = BC/TC = RC/EC

From the picture above, BR = 1.2 m, RC = 4.2 m and ER = 6.5 m

EC = ER + RC

= 6.5 + 4.2

= 10.7 m

Here BC and TC are unknown.

1.2/TE = 4.2/10.7

4.2 TE = 1.2(10.7)

TE = 1.2(10.7)/4.2

TE = 3.05 m

So, height of the tree is 3.05 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.