FINDING ORTHOCENTER OF THE TRIANGLE WITH COORDINATES

Definition of Orthocenter :

The altitudes of a triangle are concurrent and the point of concurrence is called the orthocenter of the triangle. The orthocenter is denoted by O.

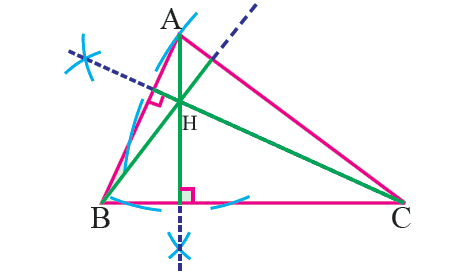
The point of intersection of the perpendicular lines drawn from the vertex A and B

Question 1:

Find the co-ordinates of the orthocentre of a triangle whose vertices are (2, -3) (8, -2) and (8, 6). 

Solution :

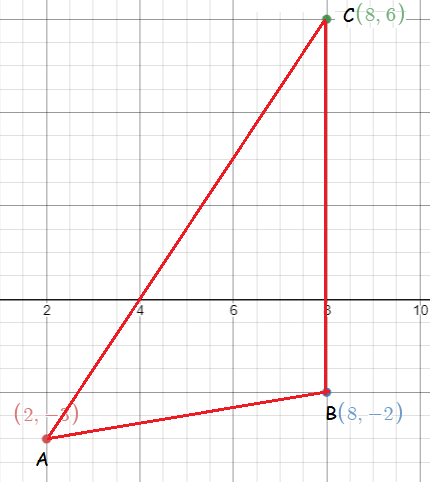
Let the given points be A (2,-3) B (8,-2) and C (8,6)

First we find the equation of perpendicular line drawn through the vertex A.

Equation of the altitude passing through A :

Slope  =  [(y₂ - y₁)/(x₂ - x₁)]

B (8, -2) and C (8, 6)

  Slope of BC  =  (6 - (-2)) / (8 - 8)

  =  8/0  =  undefined

Slope of the altitude through A = -1/ slope of BC

  =  -1/undefined

  =  0 

Here A (2, -3)  and m = 0

(y - y₁)  =  m (x - x₁)

y-(-3)  =  0 (x-2)

y + 3  =  0

Equation of the altitude passing through the vertex A is

y + 3  =  0 ---(1)

Equation of the line passing through vertex B :

A (2, -3) and C (8, 6)

Slope f AC  =  (6 + 3) / (8 - 2)

  =  9/6

=  3/2

Slope of the altitude B = -1/ slope of AC

  =  -2/3

Equation of the altitude through B :

(y - y₁)  =  m(x -x₁)

Here B (8, -2) and m  =  2/3

(y - (-2))  =  (-2/3)(x - 8)

  3 (y + 2)  =  -2 (x - 8)

  3 y + 6  =  -2 x + 16 

  2 x + 3 y - 16 + 6  =  0

  2 x + 3 y - 10  =  0 -------(2)

Orthocenter is the point of intersection of the altitudes through A and B.

By applying (1) in (2), we get

From (1), y  =  -3

2x + 3(-3) - 10  =  0

2x - 9 - 10  =  0

2x  =  19

x  =  19/2

Hence the orthocenter is (19/2, -3).

Question 2 :

Find the co-ordinates of the orthocentre of a triangle whose vertices are (3, 4) (2, -1) and (4, -6).

Solution :

Let the given points be A (3, 4) B (2, -1) and C (4, -6)

Slope of BC :

B (2, -1) and C (4, -6)

  =  (-6 + 1) / (4 - 2)

  =  -5/2

Slope of perpendicular through A  =  -1 / (-5/2)

=  2/5

Equation of altitude through the vertex A :

A(3, 4) and slope  =  2/5

(y - y₁)  =  m(x - x₁)

(y - 4)  =  (2/5)(x - 3)

5(y - 4)  =  2(x - 3)

5y - 20  =  2x - 6

2x - 5y + 20 - 6  =  0

2x - 5y  =  -14 -------(1)

Slope of AC  =  [(y₂ - y₁)/(x₂ - x₁)]

A (3, 4) and C (4, -6)

  =  (-6-4) / (4-3)

  =  -10/1

  =  -10

Slope of the altitude through B  = -1/ slope of AC

  =  -1/(-10)

  =  1/10

Equation of altitude through the vertex B :

B (2, -1) and m = 1/10

  (y - (-1))  =  (1/10) (x - 2)

  10 (y + 1)  =  (x - 2)

  10 y + 10  =  x - 2

x - 10 y - 2 - 10 = 0  

x - 10 y  =  12  --------(2)

Solving (1) and (2)

(1) - (2) ⋅ 2

        2x - 5y  =  -14

       2x - 20 y  =  24

       (-)    (+)       (-)

   --------------------

             15y  =  50

y  =  2

So the orthocentre is (-13,5/2).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.