FINDING PERCENT INCREASE

In our day to day life, often we may see the situations where the values will change. 

For example, 

Increase in wages

Increase in price of an item

Increase in temperature

In this section, we will learn the increase of a value in terms of percent. 

That is, we will calculate, how much a value is increased per hundred. 

For example, Ryan gets an hike in his salary from $3000 to $3300.

The actual increase he gets in his salary is $300. 

Here, the percent increase is, how much his salary is increased per hundred. 

In 3000, there are 30 hundreds. 

For 30 hundreds (3000), he gets an increase of 300.

Find the increase for 1 hundred.

That is,

=  300 / 30

=  10

So, for each $100 of his salary, he gets an increase of $10. 

This is called percent increase. 

Therefore, his salary is hiked by 10 percent. 

Formula

The formula given below can be used to find the percent increase of a value. 

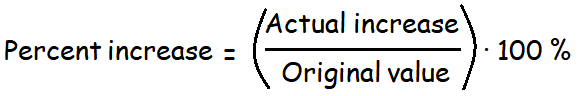
Here, the original value is the value before increase.

Practice Problems

Problem 1 : 

Due to increase in demand, the price of an item is increased from 80 cents to 1.4 dollars. Find the percentage increase in price. 

Solution :

Actual increase is

=  1.4 dollars - 80 cents

=  140 cents - 80 cents

=  60 cents

Percentage increase is  

=  (Actual increase / Original value) ⋅ 100%

=  (60 / 80) ⋅ 100%

=  75%

So, the percentage increase in price of the item is 75.

Problem 2 : 

Sally is in a long-jump competition. Her first jump and second jump are 5.6m and 6.3m respectively. Find the percentage increase in her jump length. 

Solution :

Actual increase is 

=  6.3 - 5.6

=  0.7

Percentage increase is  

=  (Actual increase / Original value) ⋅ 100%

=  (0.7 / 5.6) ⋅ 100%

=  12.5%

So, the percentage increase in her jump length is 12.5. 

Problem 3 : 

6 months ago the height of a plant was 12 inches and. The height of the plant today is 4 feet. Find the percentage change in height. 

Solution :

Actual increase is

=  4 feet - 12 inches

=  (4 ⋅ 12) inches - 12 inches

=  48 inches - 12 inches

=  36 inches

Percentage increase is  

=  (Actual increase / Original value) ⋅ 100%

=  (36 / 12) ⋅ 100%

=  3 ⋅ 100%

=  300%

So, the height of the plant is increased by 300%. 

Problem 4 : 

The length and width of a rectangle are increased by 10% and 5% respectively. Find the percentage increase in area.  

Solution :

Let l and w be the original length and width of the rectangle. 

Then, the area is lw.

After the length and width of the rectangle are increased by 10% and 5% respectively, the area is 

=  (1.1l)(1.05w)

=  1.155lw

Actual increase is 

=  1.155lw - lw

=  0.155lw

Percentage increase is  

=  (Actual increase / Original value) ⋅ 100%

=  (0.155lw / lw) ⋅ 100%

=  0.155 ⋅ 100%

=  15.5% 

So, the area of the rectangle will be increased by 15.5%.

Problem 5 : 

In a triangle, if the height is increased by 50%, what percentage of the area will be increased ?   

Solution :

Let b and h be the original base and height of the triangle respectively.

Then, the area of the triangle is

=  bh / 2

=  0.5bh

If the height is increased by 50%, then the area of the triangle is 

=  b(1.5h) / 2

=  1.5bh / 2

=  0.75bh

Actual increase is 

=  0.75bh - 0.5bh

=  0.25

Percentage increase is  

=  (Actual increase / Original value) ⋅ 100%

=  (0.25bh / 0.5bh) ⋅ 100%

=  (0.25 / 0.5) ⋅ 100%

=  50%

So, the area of the triangle will be increased by 50%.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.