FINDING PROBABILITY USING A TABLE

Recall that a compound event consists of two or more simple events. 

To find the probability of a compound event, we have to write a ratio of the number of ways the compound event can happen to the total number of equally likely possible outcomes.

Examples

Example 1 :

Jacob rolls two fair number cubes. Find the probability that the sum of the numbers he rolls is 8.

Solution :

Step 1 :

List out all the possible outcomes when two cubes are rolled. 

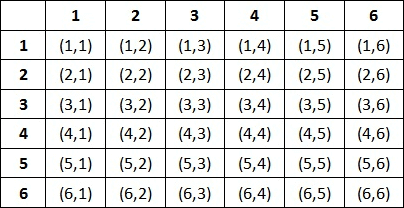
There are 36 possible outcomes in the sample space. 

Step 2 :

Create a table where each cell represents the sum on two number cubes. 

Then, circle the outcomes that give the sum of 8.

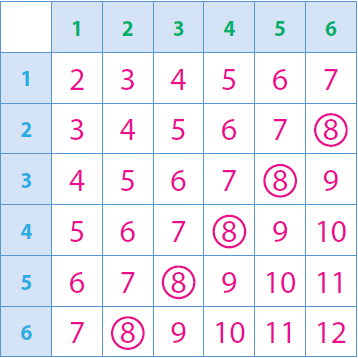
Step 3 :

Find the number of outcomes in which the sum is 8. 

Number of outcomes in which the sum is 8  =  5

Step 4 : 

Find the required probability. 

P (for sum 8)  =  5 / 36   

So, the probability that the sum of the numbers is 8 is 5/36.

Example 2 :

A six faced number cube is rolled twice. What is the probability of getting a difference of 2 ?.

Solution :

Step 1 :

List out all the possible outcomes when two cubes are rolled. 

There are 36 possible outcomes in the sample space. 

Step 2 :

List out  the outcomes where the difference between two numbers is 2. 

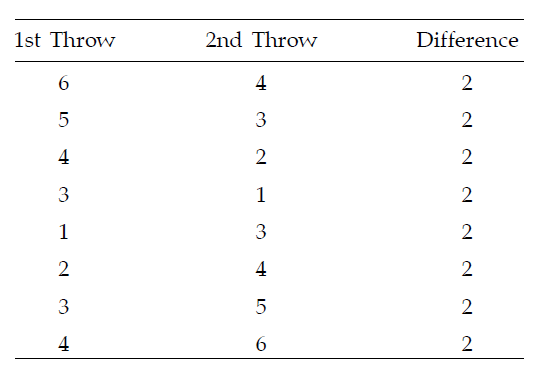
Step 3 :

Find the number of outcomes in which the difference is 2. 

Number of outcomes in which the difference is 2  =  8

Step 4 : 

Find the required probability. 

P (for difference 2)  =  8 / 36   

P (for difference 2)  =  2 / 9   

So, the probability of getting a difference of 2 is 2/9.

Example 3 :

Two dice are thrown simultaneously. Find the probability that the sum of points on the two dice would be 7 or more.

Solution : 

If two dice are thrown then, as explained in the last problem, total no. of all possible outcomes is 36.

Now a total of 7 or more i.e. 7 or 8 or 9 or 10 or 11 or 12 can occur only in the following combinations :

Sum  =  7 -----> (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)

Sum  =  8 -----> (2, 6), (3, 5), (4, 4), (5, 3), (6, 2)

Sum  =  9 -----> (3, 6), (4, 5), (5, 4), (6, 3)

Sum  =  10 -----> ((4, 6), (5, 5), (6, 4)

Sum  =  11 -----> (5, 6), (6, 5)

Sum  =  12 -----> (6, 6)

Thus the no. of favorable outcomes is 21.

Let A be the event of getting a total of 7 points or more.

Then, 

P(A)  =  21/36

P(A)  =  7/12

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.