FINDING SLOPE FROM A GRAPH

Problem 1 :

Find the slope of the line shown below. 

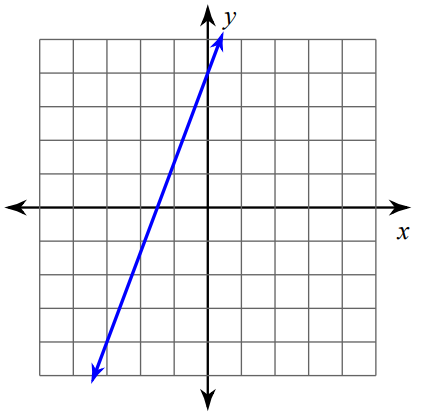
Problem 2 :

Find the slope of the line shown below. 

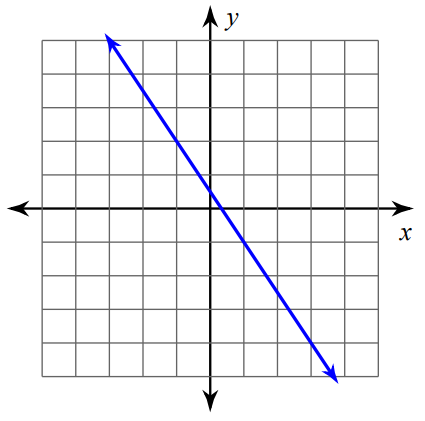
Problem 3 :

Find the slope of the line shown below. 

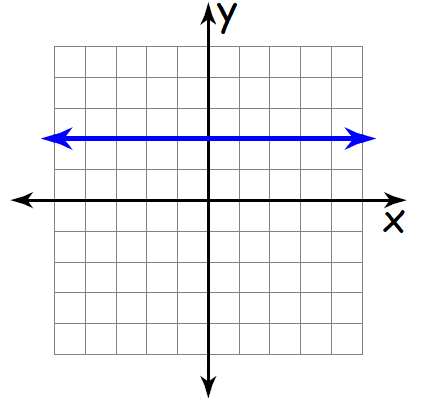
Problem 4 :

Find the slope of the line shown below. 

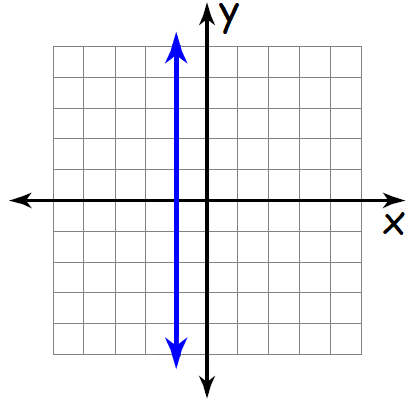
Problem 5 :

Find the slope of the line using formula. 

Problem 6 :

Find the slope of the line using formula. 

Detailed Answer Key

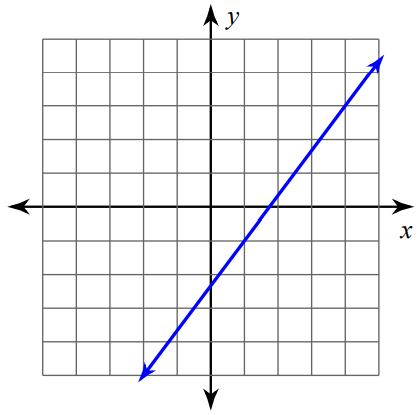
Problem 1 :

Find the slope of the line shown below. 

Solution :

The above line is a rising line. So, its slope will be a positive value.

Mark two points on the line such that both the x-coordinate and y-coordinate are integers. 

So, we can mark the points (0, 4) and (-3, -4) and measure the rise and run.

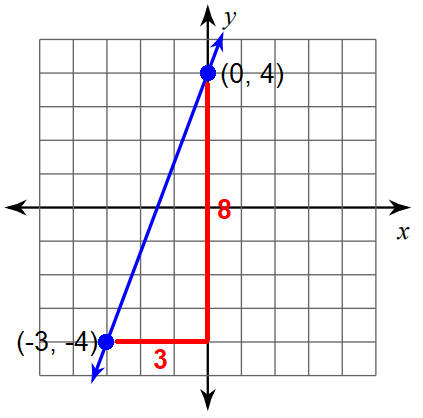
For the above line, 

Rise  =  8

Run  =  3

Then, 

Slope  =  rise / run

Slope  =  8/3

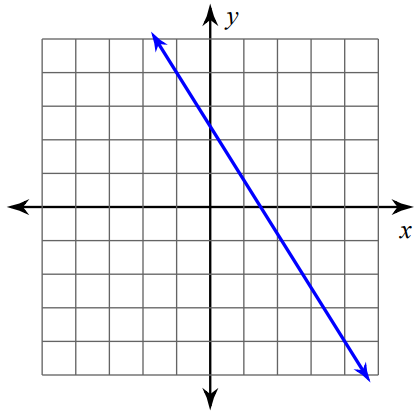
Problem 2 :

Find the slope of the line shown below. 

Solution :

The above line is a falling line. So, its slope will be a negative value.

Mark two points on the line such that both the x-coordinate and y-coordinate are integers. 

So, we can mark the points (1, -1) and (3, -4) and measure the rise and run.

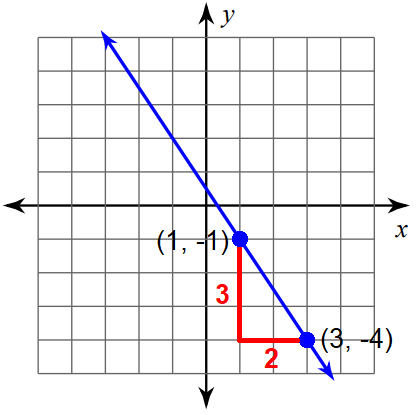
For the above line, 

Rise  =  3

Run  =  2

Then, 

Slope  =  rise / run

Slope  =  -3/2

Problem 3 :

Find the slope of the line shown below. 

Solution :

The above line is an horizontal line. 

So, its slope is zero. 

Problem 4 :

Find the slope of the line shown below. 

Solution :

The above line is a vertical line. 

So, its slope is undefined.  

Problem 5 :

Find the slope of the line using formula. 

Solution :

Mark two points on the line such that both the x-coordinate and y-coordinate are integers. 

So, we can mark the points (1, -1) and (4, 3) and measure the rise and run.

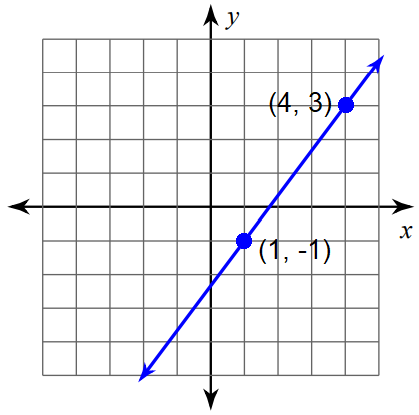
Formula :

Slope  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁) = (1, -1) and (x₂, y₂) = (4, 3). 

Slope  =  [3 - (-1)] / (4 - 1)

Slope  =  [3 + 1] / 3

Slope  =  4/3

Problem 6 :

Find the slope of the line using formula. 

Solution :

Mark two points on the line such that both the x-coordinate and y-coordinate are integers. 

So, we can mark the points (-1, 4) and (4, -4) and measure the rise and run.

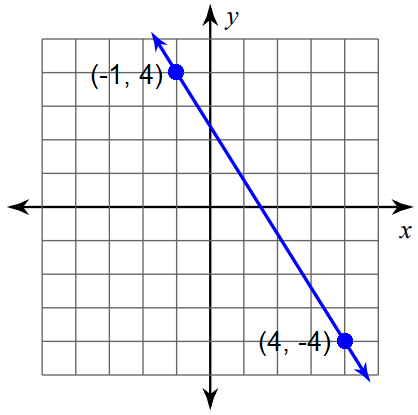
Formula :

Slope  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁) = (-1, 4) and (x₂, y₂) = (4, -4). 

Slope  =  (-4 - 4) / [4 - (-1)]

Slope  =  -8 / [4 + 1]

Slope  =  -8/5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.