FINDING SLOPE OF THE TANGENT LINE AT THE POINT USING DERIVATIVES

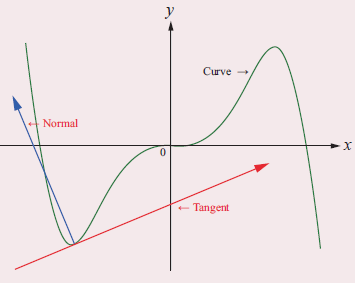
Problem 1 :

Find the slope of the tangent to the curves at the respective given points.

(i) y = x⁴ + 2x² − x at x = 1

Solution :

y = x⁴ + 2x² − x at x = 1

Slope (dy/dx)  =  4x³+4x-1

Slope at x  =  1  ==>  4(1)³+4(1)-1  ==>  7

So, slope of the tangent at x  =  1  is 7.

(ii)  x  =  a cos³t, y = b sin³t at t  =  π/2

Solution :

dy/dx  =  3asin²tsint / (-3acos²tsint)

dy/dx  =  -sint / cost

(dy/dx) at t  =  π/2

dy/dx  =  -sin (π/2) / cos (π/2)

=  1/0

dy/dx  =  ∞

So, slope of the tangent at x  =  π/2 is ∞

Problem  2 :

Find the point on the curve y = x² − 5x + 4 at which the tangent is parallel to the line 3x + y = 7 .

Solution :

Slope of the curve :

y  =  x² − 5x + 4

dy/dx  =  2x-5  -----(1)

Slope of the line :

3x+y  =  7

y  =  -3x+7

slope (m)  =  -3  ------(1)

Let (x,y) be the point where we draw the tangent line which is parallel to the given line.

(1)  =  (2)

2x-5  =  -3

2x  =  2

x  =  1

Applying x  =  1 in the equation of the curve, we get

y  =  (1)² − 5(1) + 4

y  =  0

So, the required point is (1, 0).

Problem 3 :

Find the points on the curve y = x³ − 6x² + x + 3 where the normal is parallel to the line x + y  =  1729.

Solution :

Slope of  tangent to the curve :

y  =  x³ − 6x² + x + 3

dy/dx  =  3x²-12x+1

Slope of normal to the curve :

=  -1/3x²-12x+1   ---(1)

Slope of the line :

x + y  =  1729

y  =  -x+1729

Slope (m)  =  -1  ---(2)

Let (x, y) be the point where we draw tangent line and that is parallel to the given line.

(1)  =  (2)

-1/(3x²-12x+1)  =  -1

3x²-12x+1  =  1

3x²-12x  =  0

3x(x-4)  =  0

x  =  0 and x  =  4

When x  =  0, y  =  0³ − 6(0)² + 0 + 3  ==>  3

When x  =  4, y  =  4³ − 6(4)² + 4 + 3  ==>  -25

So, the required points are (0, 3) and (4, -25).

Problem 4 :

Find the points on the curve y² - 4xy  =  x²+ 5 for which the tangent is horizontal.

Solution :

Slope of the tangent of the curve :

y² - 4xy  =  x²+ 5

2y(dy/dx) - 4[x(dy/dx) + y(1)]  =  2x

2y(dy/dx) - 4x(dy/dx) - 4y  =  2x

(dy/dx)(2y-4x)  =  2x+4y

dy/dx  =  (2x+4y)/(2y-4x)

dy/dx  =  (x+2y)/(y-2x)

Since we draw the horizontal tangent, its slope will be equal to 0.

(x+2y)/(y-2x)  =  0

x+2y  =  0

x  =  -2y

y² - 4(-2y)y  =  (-2y)²+ 5

 y² + 8y²  =  4y²+ 5

5 y²  =  5

y  =  1, -1

When y = 1, x  =  -2

When y = -1, x  =  2

So, the required points are (-2, 1) and (2, -1).

Apart from the stuff given above,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.