FINDING THE AREA OF A RHOMBUS

The area of a rhombus is half of the product of the lengths of its diagonals.

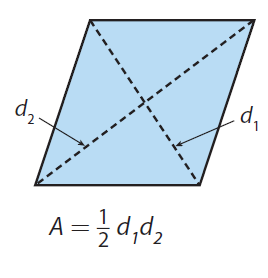
Relationship between Rhombus and Rectangle

A rhombus is a quadrilateral in which all sides are congruent and opposite sides are parallel. A rhombus can be divided into four right triangles that can then be rearranged into a rectangle.

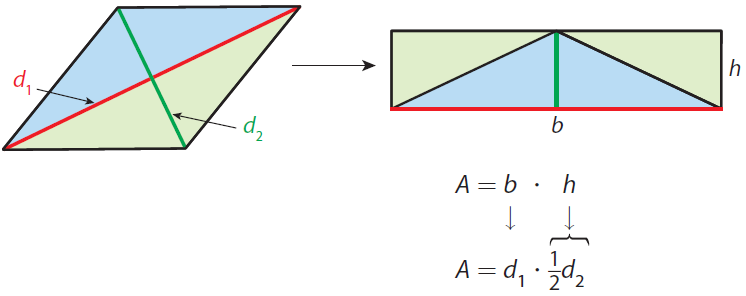
The base of the rectangle is the same length as one of the diagonals of the rhombus. The height of the rectangle is half the length of the other diagonal.

Problem 1 :

Cedric is constructing a kite in the shape of a rhombus. The spars of the kite measure 15 inches and 24 inches. How much fabric will Cedric need for the kite ?

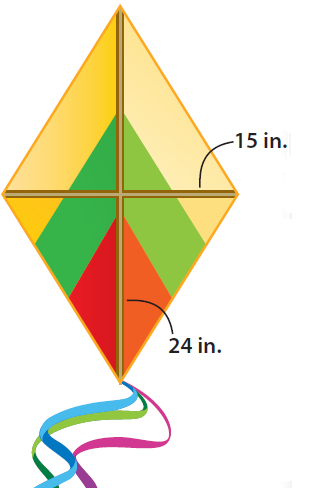
Solution :

To determine the amount of fabric needed, find the area of the kite.

Formula for area of a rhombus :

=   1/2 ⋅ (d₁d₂)

Substitute 24 for d₁ and 15 for d₂.

=   1/2 ⋅ (24 ⋅ 15)

=   12 ⋅ 15

=  180 in²

So, Cedric needs 180 square inches of fabric to make the kite.

Problem 2 :

A kite in the shape of a rhombus has diagonals that are 25 inches long and 15 inches long. What is the area of the kite?

Solution :

Formula for area of a rhombus :

=   1/2 ⋅ (d₁d₂)

Substitute 25 for d₁ and 15 for d₂.

=   1/2 ⋅ (25 ⋅ 15)

=   1/2 ⋅ (375)

=  187.5 in²

Problem 3 :

The diagonals of a rhombus are 12 in. and 16 in. long. The length of a side of the rhombus is 10 in. What is the height of the rhombus ?

Solution :

Formula for area of a rhombus :

=   1/2 ⋅ (d₁d₂)

Substitute 12 for d₁ and 16 for d₂.

=   1/2 ⋅ (12 ⋅ 16)

=   6 ⋅ 16

=  96 in²

Because rhombus is a parallelogram, we can use the formula for area of a parallelogram to find the height of the rhombus. 

Area of parallelogram  =  96 in² 

base x height  =  96

Substitute 10 for base. 

 10 x h  =  96

Divide each side by 10. 

height  =  9.6 inches

Problem 4 :

The area of a rhombus is 150 cm². The length of one of its diagonals is 10 cm. The length of the other diagonal is :

a)  25 cm   b)  30 cm   c)  35 cm    d)  40 cm

Solution :

Area of rhombus = 150 cm²

Diagonal = 10 cm

Let x be the length of the other diagonal.

 1/2 ⋅ (10 ⋅ x) = 150

5x = 150

x = 150/5

x = 30

So, the length of the other diagonal is 30 cm, option b is correct.

Problem 5 :

If the diagonals of a rhombus are 24 cm and 10 cm, the area and perimeter of the rhombus are respectively,

a)  120 cm², 52 cm           b)  120 cm², 64 cm

c)  240 cm², 52 cm           d)  240 cm², 64 cm

Solution :

Area of rhombus = 1/2 ⋅ (d₁d₂)

= (1/2) (24 x 10)

= 120 cm²

Diagonals will bisect each other at right angle.

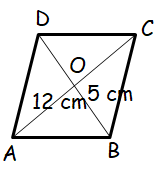
In triangle AOB,

AB² = AO² + OB²

AB² = 12² + 5²

= 144 + 25

= 169

AB = √169

AB = 13

Perimeter of rhombus = 4AB

= 4(13)

= 52 cm

So, the area of rhombus is 120 cm², 52 cm.

Problem 6 :

Each side of the rhombus are 26 cm and one of its diagonals is 48 cm long. The area of rhombus is :

a) 240 cm²    b)  300 cm²     c)  360 cm²        d) 480 cm²

Solution :

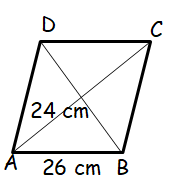
Let x be the half of the length of diagonal.

26² = 24² + x²

676 = 576 + x²

676 - 576 = x²

x² = 100

x = √100

x = 10 cm

Length of diagonal = 2(10) ==> 20 cm

Area of rhombus = (1/2) (48 x 20)

= 24 x 20

0= 480 cm²

So, option d is correct.

Problem 7 :

If the diagonals of a rhombus of side 15 cm are in the ratio 3 : 4, find the area of the rhombus.

a)  54 sq.cm     b)  108 sq.cm     c)  144 sq.cm

d)  216 sq.cm     e) none

Solution :

Side length of rhombus = 15 cm

Diagonals are in the ratio of 3 : 4

Diagonals = 3x and 4x

(3x/2)² + (2x)² = 15²

(9x²/4) + 4x² = 225

(9x² + 16x²)/4 = 225

25x²/4 = 225

x² = 225(4/25)

x² = 9(4)

x = 6

3x = 3(6) ==> 18 cm

4x = 4(6) ==> 24 cm

So, the diagonals are 18 cm and 24 cm

Area of rhombus = (1/2) (18 x 24)

= 9(24)

= 216 sq.cm

So, option d is correct.

Problem 8 :

PQRS is a rhombus perimeter is 32 cm and interior angle QRS = 120. What is the area of the rhombus PQRS ?

Solution :

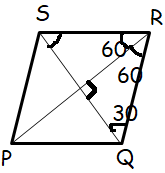
Perimeter of rhombus = 32

4a = 32

a = 32/4

a = 8

Using the concept of special right triangle,

Side opposite to 90 degree = 2(smallest side)

Let x be the side opposite to 30 degree.

2x = 8

x = 4

side opposite to 30 degree = 4

Side opposite to 60 degree = 4√3

Length of diagonal 1 = 2(4) ==> 8

Length of diagonal 2 = 2(4√3) ==> 8√3

Area of rhombus = (1/2) (8 x 8√3)

= 32√3 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.