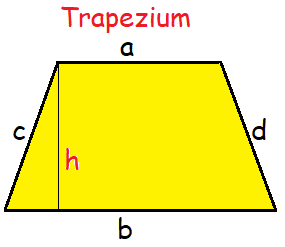
FINDING THE AREA OF A TRAPEZIUM

Formula for finding the area of a trapezium :

Area of a trapezium  =  1/2 × h (a + b) sq. units

Where,

a and b are the parallel sides (bases of trapezium),

h is the height (perpendicular distance between a and b).

Formula for finding the perimeter of a trapezium :

Perimeter of a trapezium  =  a + b + c + d units.

Problem 1 :

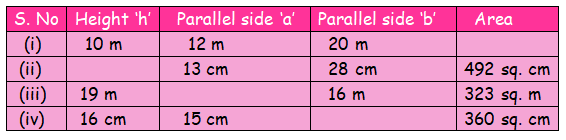
Find the missing values.

Solution :

(i)

Given, height (h)  =  10 m

Parallel sides (a)  =  12 m and (b)  =  20 m 

Area of the trapezium  =  1/2 x h (a + b) sq. units

=  1/2  x 10 (12 + 20)

=  1/2 x 10 (32)

=  160 sq. cm

Therefore, Area of the trapezium is 160 sq. cm.

(ii)

Given, Parallel sides (a)  =  13 cm and (b)  = 28 cm

Area of the trapezium  =  492 sq. cm

Area of the trapezium  =  1/2 x h (a + b) sq. units

492  =  1/2  x h (13 + 28)

 492  =  1/2 x h (41)

492 x 2  =  (h) 41

984  =  h (41)

984/41  =   h

24 cm  =  h

(iii)

Given, height (h)  =  19 m, Parallel side (b)  =  16 m 

Area of the trapezium  =  323 sq. m

Area of the trapezium  =  1/2 x h (a + b) sq. units

323  =  1/2 x 19 (a + 16)

323 x 2 =  (19a + 304)

646  =  19a + 304

646 – 304  =  19a

342  =  19a

342/19  =  a

a  =  18 m

(iv)

Given, height (h)  =  16 cm

Parallel side (a)  =  15 cm

Area of the trapezium  =  360 sq. cm

Area of the trapezium  =  1/2 x h (a + b) sq. units

360  =  1/2 x 16 (15 + b)

360 x 2  =  (240 + 16b)

720  =  240 + 16b

720 – 240  =  16b

480  =  16b

480/16  =  b

b  =  30 cm

Problem 2 :

Find the area of a trapezium whose parallel sides are 24 cm and 20 cm and the distance between them is 15 cm.

Solution :

Given, height (h)  =  15  cm

Parallel sides (a)  =  24  cm and (b)  =  20 cm 

Area of the trapezium  =  1/2 x h (a + b) sq. units

=  1/2  x 15 (24 + 20)

=  1/ 2 x 15 (44)

=  330 sq. cm

Therefore, area of a trapezium is 330 sq.cm

Problem 3 :

The area of a trapezium is 1586 sq. cm. The distance between its parallel sides is 26 cm. If one of the parallel sides is 84 cm then, find the other side.

Solution :

Given,

Area of a trapezium  =  1586 sq. cm

Height (h)  =  26 cm

One of the parallel side (a)  =  84  cm

Let, the length of the other side be ‘x’ cm.

Area of the trapezium  =  1/2 x h (a + b) sq. units

1586  =  1/2  x 26 (84 + x)

=  13 (84 + x)

1586  =  1092 + 13x

1092 + 13x  =  1586

13x  =  1586 – 1092

13x  =  494

x  =  494/13

x  =  38 cm 

Therefore, the length of the other side is 38 cm.

Problem 4 :

The area of a trapezium is 1080 sq. cm. If the lengths of its parallel sides are 55.6 cm and 34.4 cm, find the distance between them.

Solution :

Given, Parallel sides are (a)  =  55.6 cm and (b)  =  34.4 cm 

Area of the trapezium =  1080 sq. cm

Area of the trapezium  =  1/2 x h (a + b) sq. units

1080  =  1/2 x h (a + b)

1080  =  1/2 x h (55.6 + 34.4)

1080  =  1/2 x h (90)

1080  = h (45)

1080/45  =  h

24  =  h

Therefore, distance between the parallel sides is 24 cm.

Problem 5 :

The area of a trapezium is 180 sq. cm. and its height is 9 cm. If one of the parallel sides is longer than the other by 6 cm, find the length of the parallel sides.

Solution :

Given, height (h)  =  9 cm

Area of the trapezium  =  180 sq. cm

Let one of the parallel side be  ‘a’

Since the parallel of one side is longer than the other side by 6 cm,

Now, other side b  =  a + 6

Area of the trapezium  =  1/2 x h (a + b) sq. units

180  =  1/2 x 9 (a + a + 6)

180 x 2  =  9 (2a + 6)

360  =  18a + 54

360 – 54  =  18a

306  =  18a

306/18  =  a

17 cm =  a

b  =  a + 6

b  =  17 + 6

b  =  23 cm

Therefore, parallel sides (a)  =  17 cm and (b)  =  23 cm .

Problem 6 :

The sunshade of a window is in the form of isosceles trapezium whose parallel sides are 81 cm and 64 cm and the distance between them is 6 cm. Find the cost of painting the surface at the rate of $ 2 per sq. cm.

Solution :

Given, height (h)  =  6 cm

Parallel sides (a)  = 81 cm and (b)  =  64 cm

Area of the trapezium  =  1/2 x h (a + b) sq. units

=  1/2 x 6 (81 + 64)

=  1/2 x 6 (145)

A  =  435 sq. cm

Cost of painting 1 cm²  =  $2

Cost of painting 435 cm²  =  $(435 × 2)

=  435 x 2

=  $ 870

Therefore, the cost of painting  =  $ 870.

Problem 7 :

A window is in the form of trapezium whose parallel sides are 105 cm and 50 cm respectively and the distance between the parallel sides is 60 cm. Find the cost of the glass used to cover the window at the rate of $ 15 per 100 sq. cm.

Solution :

Given, height (h)  =  60 cm

Parallel sides (a)  = 105 cm and (b)  =  50 cm

Area of the trapezium  =  1/2 x h (a + b) sq. units

=  1/2 x 60 (105 + 50)

=  1/2 x 60 (155)

=  30 (155)

=  4650 sq. cm 

Cost of glass used for 100 cm²  =  $15

Cost of glass used for 4650 cm²  =  (4650/100) x 15

=  $ 697.5

Therefore, the cost of the glass used  =  $ 697.5

Apart from the stuff given above,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.