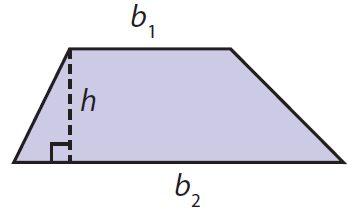
FINDING THE AREA OF A TRAPEZOID

The area of a trapezoid is half its height multiplied by the sum of the lengths of its two bases.

A  =  (1/2)h(b₁ + b₂)

Going through the history of ancient period and also that of medieval period, we do find the mention of statistics in many countries.

Relationship between Parallelogram and Trapezoid

Notice that two copies of the same trapezoid fit together to form a parallelogram. The height of the parallelogram is the same as the height of the trapezoid.

The length of the base of the parallelogram is the sum of the lengths of the two bases (b₁ and b₂) of the trapezoid.

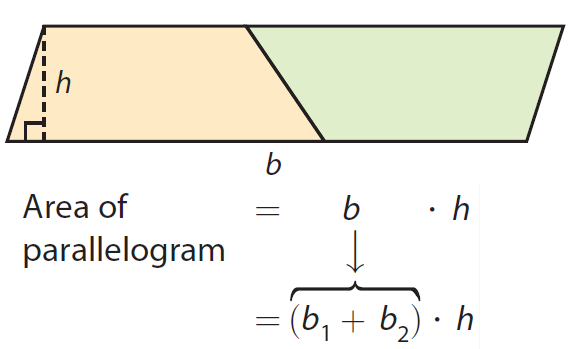
So, the area of a trapezoid is half the area of the parallelogram.

Example 1 :

A section of a deck is in the shape of a trapezoid. What is the area of this section of the

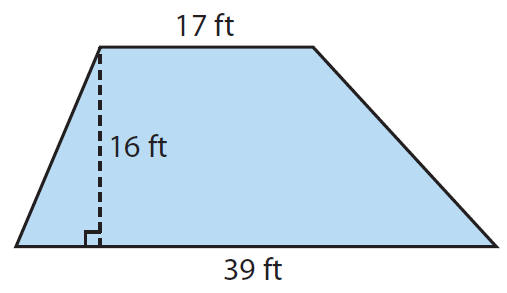
Solution :

Area of the trapezoid is

=  (1/2)h(b₁ + b₂)

Substitute b₁  =  17, b₂  =  39  and h  =  16.

  =  (1/2) x 16(17 + 39)

  =  8(56)

=  448 ft² 

Example 2 :

The length of one base of a trapezoid is 27 feet, and the length of the other base is 34 feet. The height is 12 feet. What is its area?

Solution :

Area of the trapezoid is

=  (1/2)h(b₁ + b₂)

Substitute b₁  =  27, b₂  =  34 and h  =  12.

=  (1/2) x 12(34 + 27)

=  6(61)

=  366 ft² 

Example 3 :

Simon says that to find the area of a trapezoid, you can multiply the height by the top base and the height by the bottom base. Then add the two products together and divide the sum by 2. Is Simon correct? Explain your answer.

Solution :

Yes

Simon uses the Distributive Property to multiply each base by the height. Then he finds the sum BY multiplying by 1/2 is the same as dividing by 2.

Example 4 :

The height of a trapezoid is 8 in. and its area is 96 square inches. One base of the trapezoid is 6 inches longer than the other base. What are the lengths of the bases? 

Solution :

Let 'a' and 'b' be the bases of the trapezoid.

One base of the trapezoid is 6 inches longer than the other base.

Then, 

b₁  =  b₂ + 6

Area of the trapezium  =  96 in²

(1/2)h(b₁ + b₂)  =  96

Substitute h  =  8 and b₁  =  b₂ + 6. 

(1/2) x 8(b₂ + 6 + b₂)  =  96

4(2b₂ + 6)  =  96

Divide each side by 4. 

2b₂ + 6  =  24

Subtract 2 from each side. 

2b₂  =  18

Divide each side by 2. 

b₂  =  9

Then, 

b₁  =  b₂ + 6

b₁  =  9 + 6

b₁  =  15

So, the lengths of the bases are 15 inches and cm and 9 inches. 

Example 5 :

Mr Taylor keeps chickens in the field shown. Each chicken needs 3m². What is the maximum number of chickens he can keep in the field?

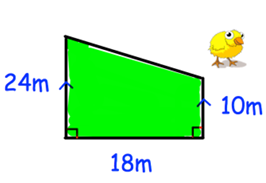
Solution :

a = 24 m, b = 10 m and height = 18 m

Area of trapezium = (1/2) x h(a + b)

= (1/2) x 18 x (24 + 10)

= 9 x 34

= 306 m²

area occupied by one chicken = 3 m²

Number of chickens = 306/3

= 102 chickens

Example 6 :

The trapezium and the triangle have the same area. Calculate the height of the triangle.

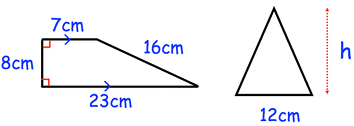
Solution :

Area of trapezium = area of triangle

(1/2) x 8 x (23 + 7) = (1/2) x 12 x h

8 x 30 = 12 x h

h = (8 x 30)/12

h = 20 cm

So, height of the triangle is 20 cm.

Example 7 :

Shown is a rectangular garden. There is a flowerbed in the shape of a trapezium. What percentage of the garden does the flowerbed cover? 

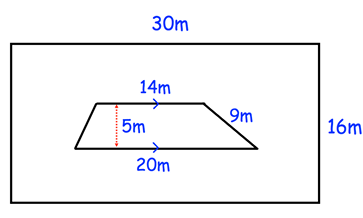
Area of rectangle outside = length x width

= 30 x 16

= 480 m²

Area of trapezium = (1/2) x 5(14 + 20)

= 2.5 x 34

= 85 cm²

Percentage = (85/480) x 100%

= 5.64 x 100%

= 564%

Example 8 :

Farmer Richards owns this field. The crop he plants earns him £7 for each square metre How much money does he earn in total?

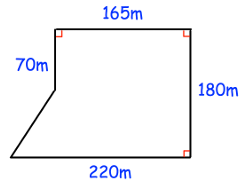
Solution :

Base of trapezium are 165 m and 220 m

height = 180 - 70

= 110 m

Area of shape given

= area of rectangle + area of trapezium

= 165 x 70 + (1/2) x 110 x (165 + 220)

= 11550 + 55 x 385

= 11550 + 21175

= 32725 m²

Required cost = 32725 x 7

= £229075

Example 9 :

A badge is made by joining two congruent trapezia. Find the area of the badge.

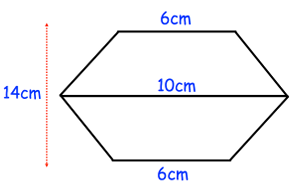
Solution :

Area of the shape given = 2 area of trapezium

Length of bases are 6 cm and 10 cm. Height = 7 cm

= 2 x (1/2) x 7 x (6 + 10)

= 7 x 16

= 112 m²

Example 10 :

A shape has been made from joining a rectangle, trapezium and triangle. The height of the shape is 3.5cm. The ratio of the height of the rectangle to the height of the trapezium to the height of the triangle is 2:3:2. Calculate the area of the

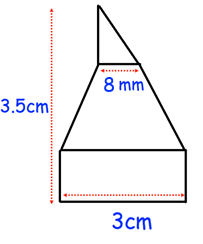
Solution :

Heights of triangle, trapezium and rectangle is in the ratio of 2 : 3 : 2

• height of triangle = 2x
• height of traepzium = 3x
• height of rectangle = 2x

2x + 3x + 2x = 3.5

7x = 3.5

x = 3.5/7

x = 0.5

2x = 2(0.5) ==> 1

3x = 3(0.5) ==> 1.5

height of triangle = 1 cm

height of trapezium = 1.5 cm

height of rectangle = 1 cm

Area of the shape

= area of triangle + area of trapezium + area of rectangle

= (1/2) x base x height + (1/2) h (a + b) + length x width

= (1/2) x 8 x 1 + (1/2) x 1.5(3 + 8) + 3 x 8

= 4 + (1/2) x 1.5 x 11 + 24

= 4 + 8.25 + 24

= 36.25 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.