FINDING THE DISTANCE BETWEEN TWO NUMBERS

To find the distance between two numbers, we have find the absolute difference between them. 

If we use number line to find the distance between them, we have to count the number of units between the two numbers. 

Example 1 : 

Find the distance between 11 and 8. 

Answer : 

Find the absolute difference : 

|11 - 8|  =  |3|  =  3

So, the distance between 11 and 8 is 3 units. 

Example 2 : 

Find the distance between -5 and 6. 

Answer : 

Find the absolute difference : 

|-5 - 6|  =  |-11|  =  11

So, the distance between -5 and 6 is 11 units. 

Example 3 : 

Find the distance between -3 and 2 using number line. 

Answer : 

Step 1 :

Mark -3 and 2 on the number line.

Step 2 :

Count the number of units between -3 and 2 as given in the picture below. 

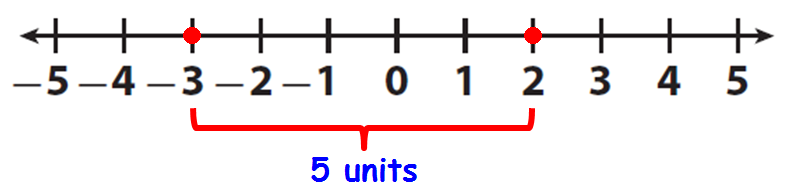
So, the distance between -3 and 2 is 5 units. 

Example 4 : 

A cave explorer climbed from an elevation of -11 meters to an elevation of -5 meters. What vertical distance did the explorer climb ?

Answer : 

Method 1 :

Start at -11.

Count the number of units on the vertical number line up to -5.

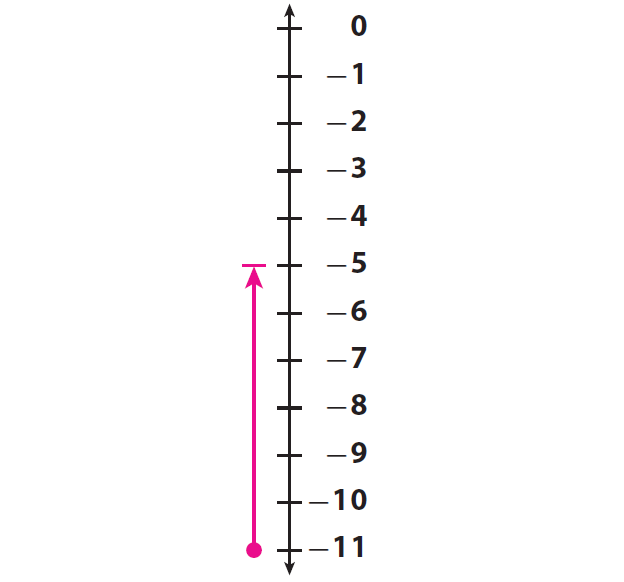
The explorer climbed 6 meters. This means that the vertical distance between -11 meters and -5 meters is 6 meters.

Method 2 :

Find the difference between the two elevations and use absolute value to find the distance.

-11 - (-5)  =  -11 + 5  =  -6 

Take the absolute value of the difference because distance traveled is always a non negative number.

|-11 - (-5)|  =  |-6|  =  6

So, the vertical distance is 6 meters. 

Example 5 :

Does it matter which way you subtract the values when finding distance ? Explain.

Answer :

No, it does not matter since you take the absolute value of the difference.

Example 6 :

Would the same methods work if both the numbers were positive ? What if one of the numbers were positive and the other negative ?

Answer :

Yes, because we take the absolute value of the difference.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.